第三期 行为规划——4.形式化FSM

让我们考虑一个简单的自动售货机，其中一切花费20美分。假设这台自动售货机只需要镍和硬币，但没有更大或更小。

然后，我们可以模拟状态这台自动售货机以已存入的金额为准。起始状态将为零美分。有两种可能发生。

我们可以投入镍，五美分或可以投入一美元，以使状态达到10美分。

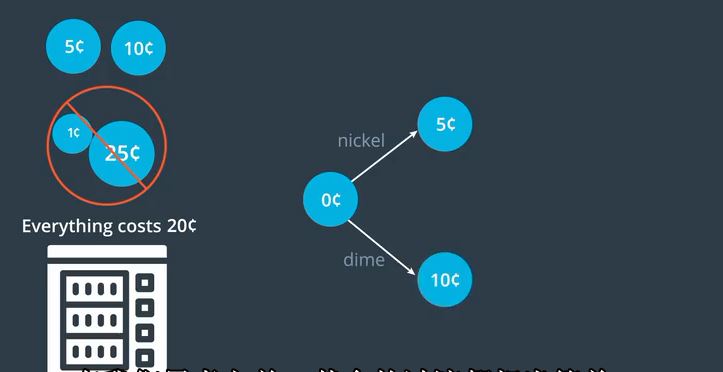
在我们思考之前，其余的过渡都相当简单。如果我们处于15美分的状态并且有人投入一毛钱该怎么办。

我们可以把它算为20。但让我们说，这台机器需要确切的变化，以便一角钱就会落下来，从机器底部的小托盘中取出。

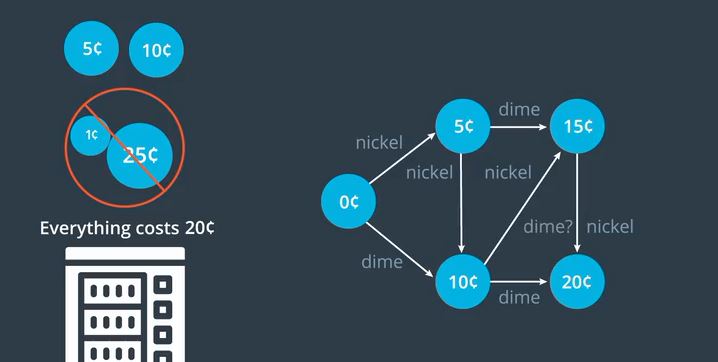
正如你所看到的，有限状态机在概念上非常简单。那么为什么要谈论他们呢？

他们有自己的长处和短处。让我们从我们的优势开始。

首先，有限状态机很容易推理。他们基本上是自我记录，因为他们映射系统的逻辑状态直接指向物理状态。

当镍进入自动售货机时状态改变为比当前状态大5美分的状态。

接下来，它们是可维护的。如果我们想调整这台机器，那么一切都会花费

如果只增加一个状态，那么四分之一的事情就会变得很微不足道。

这给我们带来了有限状态机的弱点。主要的一点是他们很容易被滥用。

如果他们没有很好地设计开始或如果问题，我们只需添加另一个状态，这可能会导致一些草率的代码和不稳定的逻辑。

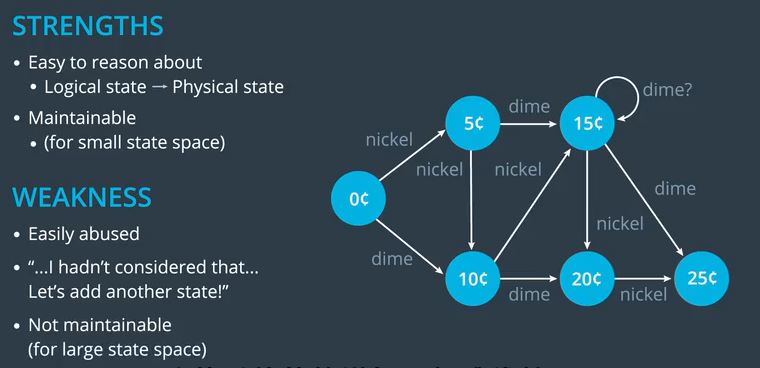
实际上这意味着有限状态机可以随着州基数的增加，很难维持。