题解【洛谷P1514】[NOIP2010]引水入城

题目描述

在一个遥远的国度，一侧是风景秀美的湖泊，另一侧则是漫无边际的沙漠。该国的行政区划十分特殊，刚好构成一个 \(N\) 行 \(M\) 列的矩形，如上图所示，其中每个格子都代表一座城市，每座城市都有一个海拔高度。

为了使居民们都尽可能饮用到清澈的湖水，现在要在某些城市建造水利设施。水利设施有两种，分别为蓄水厂和输水站。蓄水厂的功能是利用水泵将湖泊中的水抽取到所在城市的蓄水池中。因此，只有与湖泊毗邻的第 \(1\) 行的城市可以建造蓄水厂。而输水站的功能则是通过输水管线利用高度落差，将湖水从高处向低处输送。故一座城市能建造输水站的前提，是存在比它海拔更高且拥有公共边的相邻城市，已经建有水利设施。

由于第 \(N\) 行的城市靠近沙漠，是该国的干旱区，所以要求其中的每座城市都建有水利设施。那么，这个要求能否满足呢？如果能，请计算少建造几个蓄水厂；如果不能，求干旱区中不可能建有水利设施的城市数目。

输入格式

输入的每行中两个数之间用一个空格隔开。

输入的第一行是两个正整数 \(N\) 和 \(M\)，表示矩形的规模；

接下来 \(N\) 行，每行 \(M\) 个正整数，依次代表每座城市的海拔高度。

输出格式

输出有两行。

如果能满足要求，输出的第一行是整数 \(1\) ，第二行是一个整数，代表最少建造几个蓄水厂；

如果不能满足要求，输出的第一行是整数 \(0\) ，第二行是一个整数，代表有几座干旱区中的城市不可能建有水利设施。

样例

样例输入 1

2 5
9 1 5 4 3
8 7 6 1 2

样例输出 1

1
1

样例说明 1

只需要在海拔为 \(9\) 的那座城市中建造蓄水厂，即可满足要求。

样例输入 2

3 6
8 4 5 6 4 4
7 3 4 3 3 3
3 2 2 1 1 2

样例输出 2

1
3

样例说明 2

上图中，在 \(3\) 个粗线框出的城市中建造蓄水厂，可以满足要求。以这 \(3\) 个蓄水厂为源头在干旱区中建造的输水站分别用 \(3\) 种颜色标出。当然，建造方法可能不唯一。

数据范围与提示

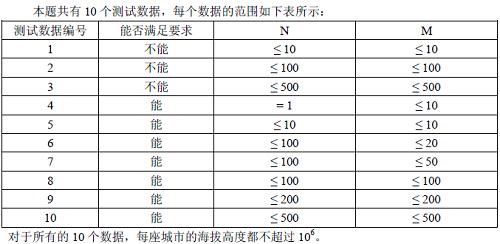
题解

考虑枚举第一行的每个位置进行\(\mathrm{DFS}\)扩展，标记已经能够覆盖到的点。

不难发现每一个点覆盖的区间都是连续的，证明留给读者作为练习。

如果一个点没有被覆盖到，说明它的海拔比它的相邻城市高。

记录每个点能够覆盖到的最左边的点\(\mathrm{l[i][j]}\)和最右边的点\(\mathrm{r[i][j]}\)，分别表示第\(i\)行第\(j\)列能够覆盖到的最左端点和最右端点。

\(\mathrm{DFS}\)的过程中更新\(\mathrm{l[i][j]}\)和\(\mathrm{r[i][j]}\)即可。

最后统计答案并输出。

具体实现细节参考代码注释。

代码

/********************************
	Author: csxsl
	Date: 2019/10/28
	Language: C++
	Problem: P1514
********************************/
#include <bits/stdc++.h>
#define itn int
#define gI gi

using namespace std;

inline int gi()
{
	int f = 1, x = 0; char c = getchar();
	while (c < '0' || c > '9') {if (c == '-') f = -1; c = getchar();}
	while (c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
	return f * x;
}

inline long long gl()
{
	long long f = 1, x = 0; char c = getchar();
	while (c < '0' || c > '9') {if (c == '-') f = -1; c = getchar();}
	while (c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
	return f * x;
}

const int maxn = 503;

int n, m, cnt, l[maxn][maxn], r[maxn][maxn], ans, a[maxn][maxn], vis[maxn][maxn];
const int dx[4] = {-1, 1, 0, 0}, dy[4] = {0, 0, 1, -1};//定义方向数组

void dfs(int x, int y)
{
	vis[x][y] = 1;//标记访问过的点，即能够覆盖到的点
	for (int i = 0; i < 4; i+=1)
	{
		int xx = x + dx[i], yy = y + dy[i];//向前后左右扩展
		if (xx < 1 || xx > n || yy < 1 || yy > m) continue;//判断边界
		if (a[xx][yy] >= a[x][y]) continue;//不能流
		if (!vis[xx][yy]) dfs(xx, yy);//进行递归
		l[x][y] = min(l[x][y], l[xx][yy]);//更新l[i][j]
		r[x][y] = max(r[x][y], r[xx][yy]);//更新r[i][j]
	}
}

int main()
{
	n = gi(), m = gi();
	memset(l, 0x3f, sizeof(l));//初始化极大值
	for (int i = 1; i <= m; i+=1) l[n][i] = r[n][i] = i;//第n行上的每个点最少能覆盖自己
	for (int i = 1; i <= n; i+=1)
	{
		for (int j = 1; j <= m; j+=1)
		{
			a[i][j] = gi();//输入海拔高度
		}
	}
	for (int i = 1; i <= m; i+=1) if (!vis[1][i]) dfs(1, i);//进行扩展
	bool fl = true;
	for (int i = 1; i <= m; i+=1) if (!vis[n][i]) {fl = false; break;}//第n行还有没被覆盖的点
	if (!fl) //不能满足要求
	{
		puts("0");
		for (int i = 1; i <= m; i+=1) if (!vis[n][i]) ++cnt;//记录不能覆盖的城市个数
		printf("%d\n", cnt);//输出
		return 0;
	}
	puts("1");//可以满足要求
	int maxleft = 1;
	while (maxleft <= m)//开始向右覆盖
	{
		int maxright = 0;
		for (int i = 1; i <= m; i+=1)
		{
			if (l[1][i] <= maxleft) maxright = max(maxright, r[1][i]);//可以覆盖当前区间
		}
		maxleft = maxright + 1;//更新新的左端点
		++cnt;//增加答案
	}
	printf("%d\n", cnt);//输出
	return 0;//结束
}