【HDU5772】String Problem [网络流]

String Problem

Time Limit: 10 Sec  Memory Limit: 64 MB
[Submit][Status][Discuss]

Description

　　

Input

　　

Output

　　

Sample Input

　　1
　　3
　　135
　　1 2
　　1 2
　　1 2
　　1 2
　　1 2
　　1 2
　　1 2
　　1 2
　　1 2
　　1 2
　　0 0 3
　　1 0 0
　　4 0 0

Sample Output

　　3

HINT

　　

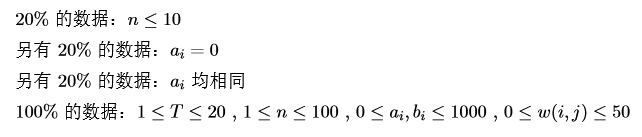
Solution

　　官方题解：

　　首先将点分为3类

　　第一类：Pij 表示第i个点和第j个点组合的点，那么Pij的权值等于w[i][j]+w[j][i]（表示得到的价值）

　　第二类：原串中的n个点每个点拆出一个点，第i个点权值为 –a[s[i]] （表示需要的花费）

　　第三类：对于10种字符拆出10个点，每个点的权值为  -(b[x]-a[x])

　　那么我们可以得到一个关系图 ，对于第一类中的点Pij，如果想要选择Pij，你就必须要选中第二类中的点i和j，对于第二类中的点如果你想选中第i个点，其对应的字符s[i]，那么就必须选中第三类中s[i] 对应的点，因为每个种类的点第一次选中时花费是b[s[i]]，而第二类中花费都是a[s[i]],一定要补上b[s[i]]-a[s[i]]，而且只需要补上一次。

　　得到上面的关系图后然后就是普通的最大权闭合子图问题,直接求解即可。

　　然后我们得到了若干关系，直接建边跑一边网络流即可。

Code

 #include<iostream>
 #include<string>
 #include<algorithm>
 #include<cstdio>
 #include<cstring>
 #include<cstdlib>
 #include<cmath>
 #include<ctime>
 using namespace std;  

 const int ONE = ;
 const int POI = ;
 const int INF = ;

 int Q,n;
 int S,T;
 char s[];
 int Val[][];
 int next[ONE],first[POI],go[ONE],w[ONE],tot;
 int Dep[POI],q[ONE],E[POI],tou,wei;
 int part1,part2,part3;
 int Ans;

 struct power
 {
         int a,b;
 }a[];

 int get()
 {
         int res=,Q=;  char c;
         while( (c=getchar())< || c>)
         if(c=='-')Q=-;
         if(Q) res=c-;
         while((c=getchar())>= && c<=)
         res=res*+c-;
         return res*Q;
 }

 void Add(int u,int v,int z)
 {
         next[++tot]=first[u];   first[u]=tot;   go[tot]=v;  w[tot]=z;
         next[++tot]=first[v];   first[v]=tot;   go[tot]=u;  w[tot]=;
 }

 int Bfs()
 {
         memset(Dep,,sizeof(Dep));
         tou=;  wei=;
         q[]=S; Dep[S]=;
         for(int i=S;i<=T;i++) E[i]=first[i];
         while(tou<wei)
         {
             int u=q[++tou];
             for(int e=first[u];e;e=next[e])
             {
                 int v=go[e];
                 if(Dep[v] || !w[e]) continue;
                 Dep[v]=Dep[u]+;
                 q[++wei]=v;
             }
         }
         return (Dep[T]>);
 }

 int Dfs(int u,int Limit)
 {
         if(u==T || !Limit) return Limit;
         int from=,f;
         for(int &e=E[u];e;e=next[e])
         {
             int v=go[e];
             if(Dep[v]!=Dep[u]+ || !w[e]) continue;
             f=Dfs(v,min(Limit,w[e]));
             w[e]-=f;
             w[((e-)^)+]+=f;
             Limit-=f;
             from+=f;
             if(!Limit) break;
         }
         return from;
 }

 void Solve()
 {
         Ans = tot = ;
         memset(first,,sizeof(first));
         n=get();
         scanf("%s",s+);
         for(int i=;i<;i++)
             a[i].a=get(), a[i].b=get();
         for(int i=;i<=n;i++)
         for(int j=;j<=n;j++)
             Val[i][j]=get(); 

         part1 = n*(n-)/;    part2 = n;    part3 = ;
         S=;    T= part1 + part2 + part3 +;
         int num = ;
         for(int i=;i<=n;i++)
         for(int j=i+;j<=n;j++)
         {
             num ++;    Ans += Val[i][j]+Val[j][i];
             Add(S,num, Val[i][j]+Val[j][i]);
             Add(num,part1+i, INF);
             Add(num,part1+j, INF);
         }

         for(int i=;i<=n;i++)
         {
             Add(part1+i,T, a[s[i]-''].a);
             Add(part1+i,part1+part2+s[i]-''+, INF);
         }

         for(int i=;i<;i++)
             Add(part1+part2+i+,T, a[i].b-a[i].a);

         while(Bfs()) Ans-=Dfs(S,INF);

         printf("%d\n",Ans);
 }

 int main()
 {
         Q=get();
         while(Q--)
             Solve();
 }