拟牛顿法——DFP、BFGS、L-BFGS
DFP
该算法的核心是：通过迭代的方法，对Hk+1(-1)近似。迭代方式：
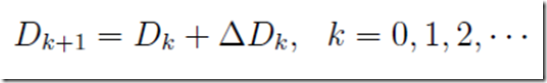
其中D0通常取为单位矩阵，关键是每一步构造矫正矩阵△Dk。
考虑△Dk 的待定形式为
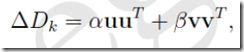
拟牛顿的条件
这里插播一下拟牛顿的条件。
前面有讲到，拟牛顿法是想找到一个近似矩阵D来近似海森矩阵H的逆。显然D的选择是必须有条件的。为了表示清楚，下文B≈H,D≈H-1
设经过k+1次迭代后得到Xk+1,此时将目标函数在Xk+1附近作泰勒展开，取二阶近似，得到
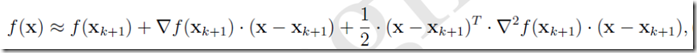
对其两边作用一个梯度算子▽，可得
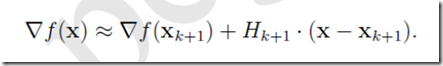
在上式中取X=Xk,并整理得到
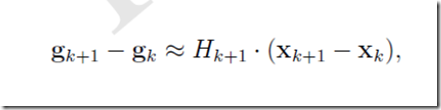
若引入记号
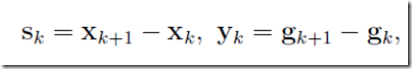
则有
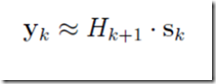或者
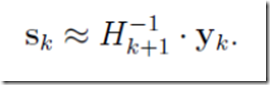
这就是所谓的拟牛顿条件对于我们的近似矩阵B或D则有
有了这个拟牛顿条件我们就能开始构造D了
构造矩阵D
结合两式：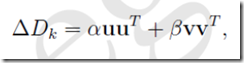
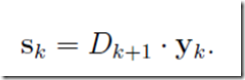
则有
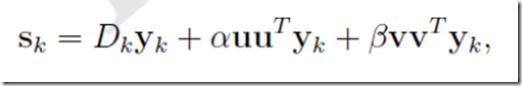
并且可以写成
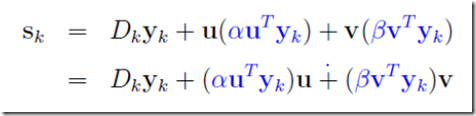
由于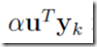
和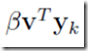
是两个数，且里面α和β在里面起到类似放缩的作用，不妨假设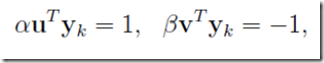
即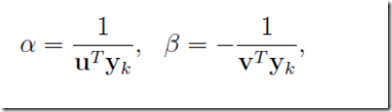
其中u，v仍是待定的
可以得到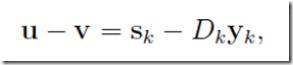
不妨直接取
则有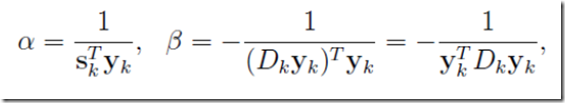
至此则有
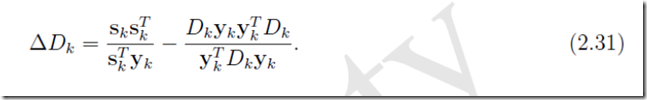
注：这里的（1.13）公式为
这里gk表示一阶导。
待更新！！
拟牛顿法——DFP、BFGS、L-BFGS的更多相关文章
- 牛顿法与拟牛顿法，DFP法，BFGS法，L-BFGS法
牛顿法 考虑如下无约束极小化问题: $$\min_{x} f(x)$$ 其中$x\in R^N$,并且假设$f(x)$为凸函数,二阶可微.当前点记为$x_k$,最优点记为$x^*$. 梯度下降法用的是 ...
- 牛顿法|阻尼牛顿法|拟牛顿法|DFP算法|BFGS算法|L-BFGS算法
一直记不住这些算法的推导,所以打算详细点写到博客中以后不记得就翻阅自己的笔记. 泰勒展开式 最初的泰勒展开式,若 在包含 的某开区间(a,b)内具有直到n+1阶的导数,则当x∈(a,b)时,有: ...
- 牛顿法/拟牛顿法/DFP/BFGS/L-BFGS算法
在<统计学习方法>这本书中,附录部分介绍了牛顿法在解决无约束优化问题中的应用和发展,强烈推荐一个优秀博客. https://blog.csdn.net/itplus/article/det ...
- 拟牛顿法/Quasi-Newton，DFP算法/Davidon-Fletcher-Powell，及BFGS算法/Broyden-Fletcher-Goldfarb-Shanno
拟牛顿法/Quasi-Newton,DFP算法/Davidon-Fletcher-Powell,及BFGS算法/Broyden-Fletcher-Goldfarb-Shanno 转载须注明出处:htt ...
- 最优化算法【牛顿法、拟牛顿法、BFGS算法】
一.牛顿法 对于优化函数\(f(x)\),在\(x_0\)处泰勒展开, \[f(x)=f(x_0)+f^{'}(x_0)(x-x_0)+o(\Delta x) \] 去其线性部分,忽略高阶无穷小,令\ ...
- 牛顿法与拟牛顿法学习笔记（四）BFGS 算法
机器学习算法中经常碰到非线性优化问题,如 Sparse Filtering 算法,其主要工作在于求解一个非线性极小化问题.在具体实现中,大多调用的是成熟的软件包做支撑,其中最常用的一个算法是 L-BF ...
- 牛顿法与拟牛顿法学习笔记（三）DFP 算法
机器学习算法中经常碰到非线性优化问题,如 Sparse Filtering 算法,其主要工作在于求解一个非线性极小化问题.在具体实现中,大多调用的是成熟的软件包做支撑,其中最常用的一个算法是 L-BF ...
- 牛顿法与拟牛顿法学习笔记（五）L-BFGS 算法
机器学习算法中经常碰到非线性优化问题,如 Sparse Filtering 算法,其主要工作在于求解一个非线性极小化问题.在具体实现中,大多调用的是成熟的软件包做支撑,其中最常用的一个算法是 L-BF ...
- <转>牛顿法与拟牛顿法
转自:http://blog.csdn.net/itplus/article/details/21896619 机器学习算法中经常碰到非线性优化问题,如 Sparse Filtering 算法,其主要 ...
随机推荐
- URAL 1750 Pakhom and the Gully 计算几何+floyd
题目链接:点击打开链接 gg.. . #pragma comment(linker, "/STACK:1024000000,1024000000") #include <cs ...
- Creating Dialogbased Windows Application (2) / 创建基于对话框的Windows应用程序（二）Button的应用、新建子窗体 / VC++, Windows
创建基于对话框的Windows应用程序(二) —— Button的应用.新建子窗体 可以发现上一节创建的窗体中,点击OK和Cancel两个按钮是没有任何反应的.现在我们来为他们添加退出对话框的功能. ...
- Windows.form增删改查
主界面 using System;using System.Collections.Generic;using System.ComponentModel;using System.Data;usin ...
- Flex读取txt文件里的内容报错
Flex读取txt文件里的内容 1.详细错误例如以下 2.错误原因 读取文件不存在 var file:File = new File(File.applicationDirectory.nativeP ...
- Java获取系统安装软件列表
/** * @author <a href="mailto:foohsinglong@gmail.com">kevin.long</a> * @descri ...
- input子系统分析（转）
转自:http://www.linuxidc.com/Linux/2011-09/43187.htm 作者:作者:YAOZHENGUO2006 Input子系统处理输入事务,任何输入设备的驱动程序都可 ...
- 2017 Wuhan University Programming Contest (Online Round) C. Divide by Six 分析+模拟
/** 题目:C. Divide by Six 链接:https://oj.ejq.me/problem/24 题意:给定一个数,这个数位数达到1e5,可能存在前导0.问为了使这个数是6的倍数,且没有 ...
- 光圈与F数相关知识
一.F数 F数.光圈数.相对孔径的倒数. F数代表的意义 F数小(光圈大).F数大(光圈小). F数又称为镜头速度,F数小的镜头速度快.因为拍摄的曝光时间△t 正比于F数的平方. F数还能表征镜头的分 ...
- 在Amazon cloud 升级CentOS5.4 到 5.9
升级前一定要备份重要资料,做好最坏的打算,最好的准备! 老板不知道为什么,喜欢升级服务器,劝过好几次都坚持要升级. 好吧,you are boss. 升级前当然免不了google一番.发现CentOS ...
- 转载：给bash的提示符设置不同的颜色 一个很常用的功能，效果如下：
原文来自:http://www.cnblogs.com/cyttina/archive/2013/01/08/2850406.html 一个很常用的功能,效果如下: 这样就可以很轻易的将输入的指令和其 ...