git的基本操作总结

参考链接

https://blog.csdn.net/u012661010/article/details/73433872

https://blog.csdn.net/shj_php/article/details/78109916

https://blog.csdn.net/weixin_42152081/article/details/80635777   # 删除github上已有的仓库

步骤一：先在github上注册一个账号，接着创建自己的仓库

打开github官网：https://github.com/

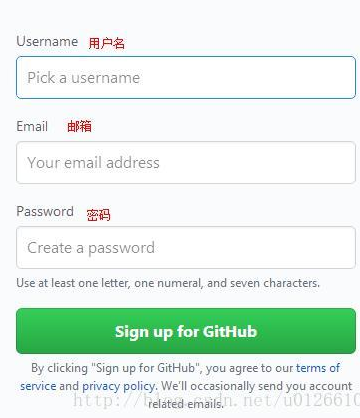
注册完成之后登录上去，创建自己的仓库

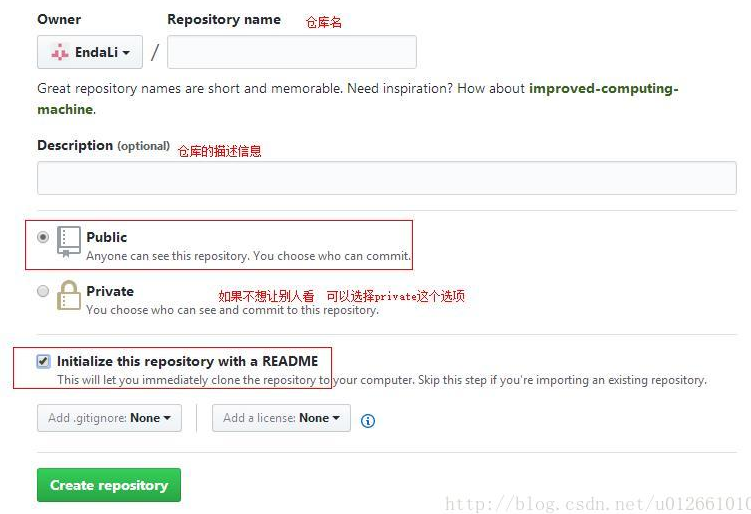
步骤二：安装git这个软件

下载地址：http://windows.github.com/
安装完成之后，就可以进行下面的操作了。

步骤三：先把自己的代码仓库克隆下来

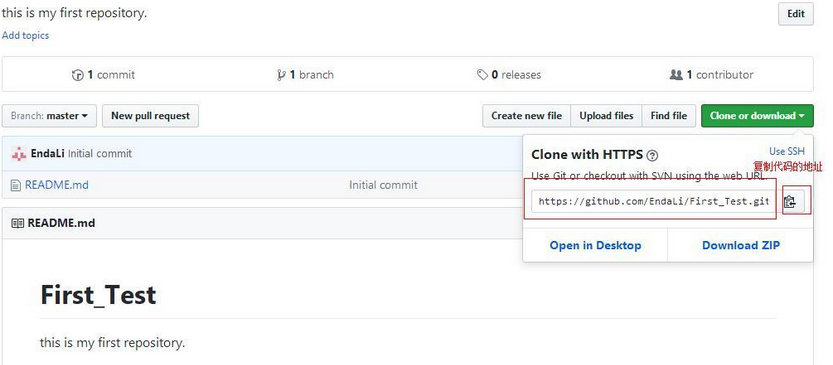
在自己所在项目文件夹上鼠标右键，点击“git bash here ”

接着输入

git clone 仓库地址

步骤四：项目上传到仓库

1.在项目所在的目录上鼠标右键点击git bash here，输入git init，意思是在当前项目的目录中生成本地的git管理（会发现在当前目录下多了一个.git文件夹，这个文件为隐藏文件）

2.输入git add.  ，这个是将项目上所有的文件添加到仓库中的意思，如果想添加某个特定的文件，只需把.换成这个特定的文件名即可。

3.输入git commit -m ‘first commit’ ，表示你对这次提交的注释，双引号里面的内容可以根据个人的需要改。

注意：这里要额外做个插曲！！！ -- 创建SSH KEY

先看一下你C盘用户目录下有没有.ssh目录，有的话看下里面有没有id_rsa和id_rsa.pub这两个文件，有就跳到下一步，没有就通过下面命令创建

$ ssh-keygen -t rsa -C "youremail@example.com"

然后一路回车。这时你就会在用户下的.ssh目录里找到id_rsa和id_rsa.pub这两个文件

登录Github,找到右上角的图标，打开点进里面的Settings，再选中里面的SSH and GPG KEYS，点击右上角的New SSH key，然后Title里面随便填，再把刚才id_rsa.pub里面的内容复制到Title下面的Key内容框里面，最后点击Add SSH key，这样就完成了SSH Key的加密。具体步骤也可看下面

4.输入git remote add origin 自己的仓库地址，将本地仓库关联到github上

ps：出现错误

fatal: remote origin already exists

则执行以下语句

git remote rm origin

再次执行

git remote add origin 自己仓库地址

5.输入git push -u origin master，把代码上传到github仓库。执行完后，输入username和password即可

坑点一：将本地仓库内容推送到远程仓库的时候就会报一个failed to push some refs to  https://github.com/guyibang/TEST2.git的错。

报错原因：在创建远程仓库的时候，勾选了Initialize this repository with a README（就是创建仓库的时候自动给你创建一个README文件），但是新创建的那个仓库里面的README文件不在本地仓库目录中

解决方法：将内容合并，

git pull --rebase origin master

git remote add origin 自己仓库地址