AVL的旋转
转自http://blog.csdn.net/gabriel1026/article/details/6311339
平衡二叉树在进行插入操作的时候可能出现不平衡的情况,AVL树即是一种自平衡的二叉树,它通过旋转不平衡的节点来使二叉树重新保持平衡,并且查找、插入和删除操作在平均和最坏情况下时间复杂度都是O(log n)
AVL树的旋转一共有四种情形,注意所有旋转情况都是围绕着使得二叉树不平衡的第一个节点展开的。
1. LL型
平衡二叉树某一节点的左孩子的左子树上插入一个新的节点,使得该节点不再平衡。这时只需要把树向右旋转一次即可,如图所示,原A的左孩子B变为父结点,A变为其右孩子,而原B的右子树变为A的左子树,注意旋转之后Brh是A的左子树(图上忘在A于Brh之间标实线)
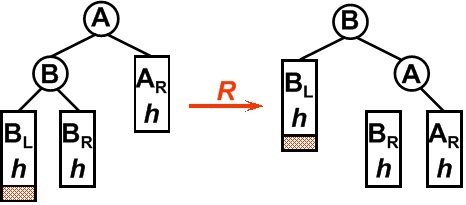
2. RR型
平衡二叉树某一节点的右孩子的右子树上插入一个新的节点,使得该节点不再平衡。这时只需要把树向左旋转一次即可,如图所示,原A右孩子B变为父结点,A变为其左孩子,而原B的左子树Blh将变为A的右子树。
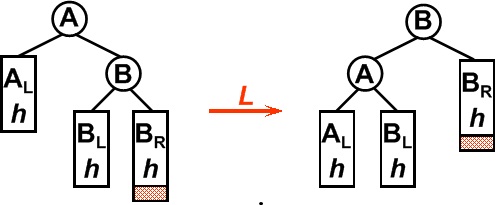
3. LR型
平衡二叉树某一节点的左孩子的右子树上插入一个新的节点,使得该节点不再平衡。这时需要旋转两次,仅一次的旋转是不能够使二叉树再次平衡。如图所示,在B节点按照RR型向左旋转一次之后,二叉树在A节点仍然不能保持平衡,这时还需要再向右旋转一次。
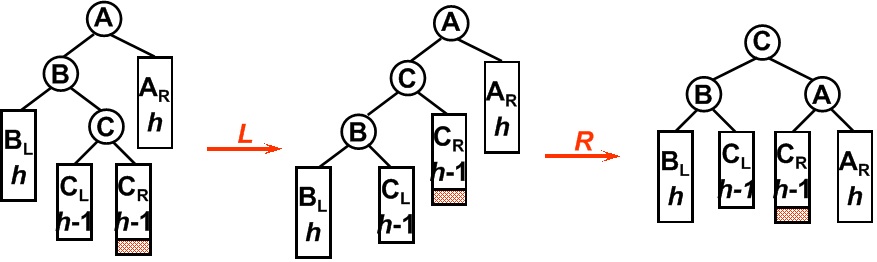
4. RL型
平衡二叉树某一节点的右孩子的左子树上插入一个新的节点,使得该节点不再平衡。同样,这时需要旋转两次,旋转方向刚好同LR型相反。
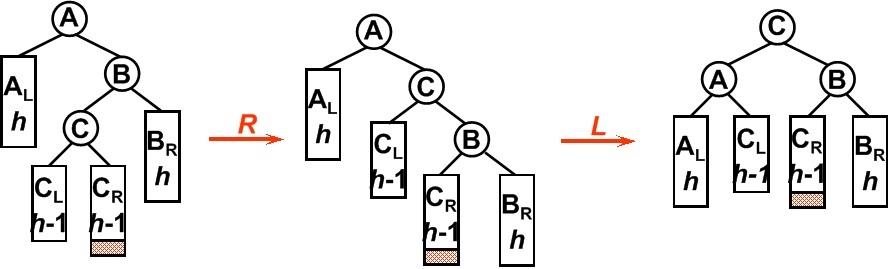
AVL的旋转的更多相关文章
- 我的新发现:AVL树旋转的一个特性
关于AVL树旋转的代码网络上铺天盖地. 一些经典的实现方法如下: AVLTree SingleLeftRotation(AVLTree A) { AVLTree B = A->left; A-& ...
- AVL树旋转
什么是AVL树? AVL树是带有平衡条件的二叉查找树,一颗AVL树首先是二叉查收树(每个节点如果有左子树或右子树,那么左子树中数据小于该节点数据,右子树数据大于该节点数据),其次,AVL树必须满足平衡 ...
- (精)AVL树旋转共8种情况(涵盖所有考研的范围)
- PAT树_层序遍历叶节点、中序建树后序输出、AVL树的根、二叉树路径存在性判定、奇妙的完全二叉搜索树、最小堆路径、文件路由
03-树1. List Leaves (25) Given a tree, you are supposed to list all the leaves in the order of top do ...
- AVL树的插入与删除
AVL 树要在插入和删除结点后保持平衡,旋转操作必不可少.关键是理解什么时候应该左旋.右旋和双旋.在Youtube上看到一位老师的视频对这个概念讲解得非常清楚,再结合算法书和网络的博文,记录如下. 1 ...
- 详解什么是平衡二叉树(AVL)(修订补充版)
详解什么是平衡二叉树(AVL)(修订补充版) 前言 Wiki:在计算机科学中,AVL树是最早被发明的自平衡二叉查找树.在AVL树中,任一节点对应的两棵子树的最大高度差为1,因此它也被称为高度平衡树.查 ...
- 什么是平衡二叉树(AVL)
前言 Wiki:在计算机科学中,AVL树是最早被发明的自平衡二叉查找树.在AVL树中,任一节点对应的两棵子树的最大高度差为1,因此它也被称为高度平衡树.查找.插入和删除在平均和最坏情况下的时间复杂度都 ...
- AVL树总结
定义:一棵AVL树或者是空树,或者是具有下列性质的二叉搜索树:它的左子树和右子树都是AVL树,且左右子树的高度之差的绝对值不超过1 AVL树失衡旋转总结: 假如以T为根的子树失衡.定义平衡因子为 H( ...
- AVL树(平衡二叉树)
定义及性质 AVL树:AVL树是一颗自平衡的二叉搜索树. AVL树具有以下性质: 根的左右子树的高度只差的绝对值不能超过1 根的左右子树都是 平衡二叉树(AVL树) 百度百科: 平衡二叉搜索树(Sel ...
随机推荐
- SharePoint 2010/SharePoint 2013 Custom Action: 基于Site Collection 滚动文字的通知.
应用场景: 有时候我们的站点需要在每个页面实现滚动文字的通知,怎么在不修改Master Page的情况下实现这个功能?我们可以使用Javascript 和 Custom Action 来实现. 创建一 ...
- 【转载】link和@import的区别
link和@import的区别 原文地址:http://www.cnblogs.com/zbo/archive/2010/11/17/1879590.html 页面中使用CSS的方式主要有3种:行内添 ...
- VBS基础篇 - FileSystemObject对象
文件系统是所有操作系统最重要的部分之一,脚本经常会需要对文件及文件夹进行访问和管理,在Vbs中对桌面和文件系统进行访问的顶级对象是FileSystemObject FSO包含的常见对象有: ...
- 《Dive into Python》Chapter 2 and Chapter 3 笔记
Example 2.1. odbchelper.py def buildConnectionString(params): """Build a connection s ...
- diahosting的低配vps弱爆了
以下仅为一个用户的心声 上年年中的时候买了dia的128M vps,算是我第一个vps.工作以来,我弄了一个wp博客,所以我在上面搭了apache的服务器,但是由于内存低,挂得也快.后来我换了Ngin ...
- ViewController 优化
解决问题:部分复杂页面的Controller过于庞大,不利于维护与复用: 复杂的页面大多是基于tableview的页面.复杂页面的代码大致可分为两部分(复杂的View布局用Nib实现的话,一般大家都是 ...
- 【POJ】【1739】Tony's Tour
插头DP 楼教主男人八题之一! 要求从左下角走到右下角的哈密顿路径数量. 啊嘞,我只会求哈密顿回路啊……这可怎么搞…… 容易想到:要是把起点和重点直接连上就变成一条回路了……那么我们就连一下~ 我们可 ...
- [spring]启动时报错:NoSuchMethodError: javax.servlet.http.HttpServletResponse.getStatus()I
Spring V4.1以后的版本在不支持Servlet3.0的应用服务器上跑时会报如下错误: NoSuchMethodError: javax.servlet.http.HttpServletResp ...
- Http、tcp、Socket连接区别
转自Http.tcp.Socket连接区别 相信不少初学手机联网开发的朋友都想知道Http与Socket连接究竟有什么区别,希望通过自己的浅显理解能对初学者有所帮助. 1.TCP连接 要想明白Sock ...
- HDOJ 1856 More is better
转自:wutianqi http://www.wutianqi.com/?p=1069 tag:并查集 #include <iostream> using namespace std; # ...
