AtCoder Grand Contest 017 F - Zigzag

题目传送门：https://agc017.contest.atcoder.jp/tasks/agc017_f

题目大意：

找出\(m\)个长度为\(n\)的二进制数，定义两个二进制数的大小关系如下：若\(a<b\)，则设\(a_i\)表示\(a\)的二进制下第\(i\)位（从左往右）的数，有\(a_i\leqslant b_i,i\in[1,n]\)

现需要满足每个二进制数需要小于其之后的二进制数，并且给出一些性质，满足第\(A_j\)个二进制数的第\(B_j\)位（从左往右）必须要为\(C_i\)，求方案数

---

显然是个DP题，考虑如何DP，我们首先可以想到状压每条路径，设\(f_{i,j}\)表示当前走完第\(i\)条路径，第\(i\)条路径的表示为\(j\)，转移时直接枚举下一条路径，时间复杂度\(O(2^{2·N}·M)\)，枚举子集优化可以为\(O(3^N·M)\)，但无论如何都过不了

考虑优化，上一个DP做法的瓶颈在于需要枚举下一条路径的状态，我们考虑不枚举，直接从当前状态下手。设\(f_{i,j,k}\)表示当前正在走第\(i\)条路径，已经走了\(j\)步，目前能走的最靠左的路径状态为\(k\)

我们枚举第\(j+1\)步向哪边移动，如果要向左走，当前位置状态必须为\(0\)；如果向右走，当前位置状态为\(1\)时直接走，如果当前位置状态不为零，就把后面位置的一个\(1\)挪到这里，用位运算可以做到\(O(1)\)转移，复杂度\(O(2^N·N·M)\)

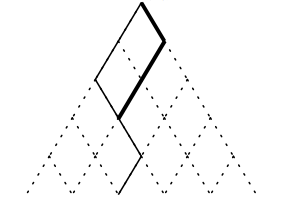
(细线为原本路径，粗线为新路径，相当于将后面的一个\(1\)提前了)

/*program from Wolfycz*/
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define inf 0x7f7f7f7f
#define lowbit(x) ((x)&-(x))
using namespace std;
typedef long long ll;
typedef unsigned int ui;
typedef unsigned long long ull;
inline char gc(){
	static char buf[1000000],*p1=buf,*p2=buf;
	return p1==p2&&(p2=(p1=buf)+fread(buf,1,1000000,stdin),p1==p2)?EOF:*p1++;
}
inline int frd(){
	int x=0,f=1; char ch=gc();
	for (;ch<'0'||ch>'9';ch=gc())	if (ch=='-')	f=-1;
	for (;ch>='0'&&ch<='9';ch=gc())	x=(x<<3)+(x<<1)+ch-'0';
	return x*f;
}
inline int read(){
	int x=0,f=1; char ch=getchar();
	for (;ch<'0'||ch>'9';ch=getchar())	if (ch=='-')	f=-1;
	for (;ch>='0'&&ch<='9';ch=getchar())	x=(x<<3)+(x<<1)+ch-'0';
	return x*f;
}
inline void print(int x){
	if (x<0)	putchar('-'),x=-x;
	if (x>9)	print(x/10);
	putchar(x%10+'0');
}
const int p=1e9+7;
int f[2][(1<<20)+10],C[30][30];
int main(){
	int n=read()-1,m=read(),k=read();
	for (int i=1;i<=k;i++){
		int x=read(),y=read(),z=read();
		C[x][y-1]=z+1;
	}
	f[0][0]=1; int now=0;
	for (int i=1;i<=m;i++){
		for (int j=0;j<n;j++){
			now^=1;
			memset(f[now],0,sizeof(f[now]));
			for (int s=0;s<1<<n;s++){
				if (f[now^1][s]){
					if (C[i][j]!=2&&((s>>j)&1)==0)	f[now][s]=(f[now][s]+f[now^1][s])%p;
					if (C[i][j]!=1){
						int Ns=0;
						if ((s>>j)&1)	Ns=s;
						else{
							int tmp=((-1)^((1<<(j+1))-1))&s,Ds=!tmp?0:lowbit(tmp);
							Ns=s^(1<<j)^Ds;
						}
						f[now][Ns]=(f[now][Ns]+f[now^1][s])%p;
					}
				}
			}
		}
	}
	int Ans=0;
	for (int s=0;s<1<<n;s++)	Ans=(Ans+f[now][s])%p;
	printf("%d\n",Ans);
	return 0;
}