ACM数论-求组合数

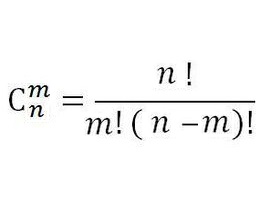
我们利用这个公式求阶乘和逆元求阶：

#include<cstdio>
const int N = 200000 + 5;
const int MOD = (int)1e9 + 7;
int F[N], Finv[N], inv[N];//F是阶乘，Finv是逆元的阶乘
void init(){
    inv[1] = 1;
    for(int i = 2; i < N; i ++){
        inv[i] = (MOD - MOD / i) * 1ll * inv[MOD % i] % MOD;
    }
    F[0] = Finv[0] = 1;
    for(int i = 1; i < N; i ++){
        F[i] = F[i-1] * 1ll * i % MOD;
        Finv[i] = Finv[i-1] * 1ll * inv[i] % MOD;
    }
}
int comb(int n, int m){//comb(n, m)就是C(n, m)
    if(m < 0 || m > n) return 0;
    return F[n] * 1ll * Finv[n - m] % MOD * Finv[m] % MOD;
}
int main(){
    init();
    printf("%d\n",comb(5,1));
    return 0;
}