优化问题及KKT条件

整理自其他优秀博文及自己理解。

目录

• 无约束优化
• 等式约束
• 不等式约束（KKT条件）

1、无约束优化

无约束优化问题即高数下册中的 “多元函数的极值"  部分。

驻点：所有偏导数皆为0的点；

极值点：在邻域内最大或最小的点；

最值点：在定义域内最大或最小的点；

关系：

驻点不一定是极值点，极值点一定是驻点；

极值点不一定是最值点，最值点一定是极值点；

求解最值：

求出所有的极值点，将所有的极值点带入函数中，最大或最小的那个就是最值点。

2、等式约束

等式约束问题即高数下册中的 “条件极值  拉格朗日乘数法” 部分。

对于$z=f(x,y)$在$\varphi(x,y)=0$的条件下的最值问题：

构造拉格朗日函数：$L(x,y,\lambda)=f(x,y)+\lambda\varphi(x,y)$；

对拉格朗日函数求解，得到的即为在条件$\varphi(x,y)=0$下，$z=f(x,y)$所有可能的极值点。再利用问题本身的其他约束条件（如果有的话）筛选极值点，比较之后求得最值点。

直观的解释：目标函数和约束函数在最优解处的法线共线，即$\bigtriangledown f(x,y)=\lambda\bigtriangledown g(x,y)$

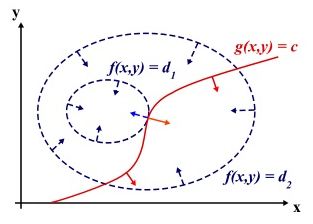
具体证明请查阅高数课本。

3、不等式约束

当约束是不等式的时候，可以在不等式约束中加入松弛变量，使其变为等式约束问题，再进行一些分析。

最后$x^*$是极值点的必要条件（KKT条件）为：

$f(x)=\left\{
\begin{aligned}
\bigtriangledown f(x) & = & \lambda \bigtriangledown c_i(x) \\
\lambda_ic_i(x) & = & 0\\
\lambda_i & \geq & 0
\end{aligned}
\right.$

不等式约束可以直接利用KKT条件求出可能的极值点。

具体推导和证明可参见：https://zhuanlan.zhihu.com/p/26514613

他们之间的关系：（此图来自知乎上链接，入侵可删）

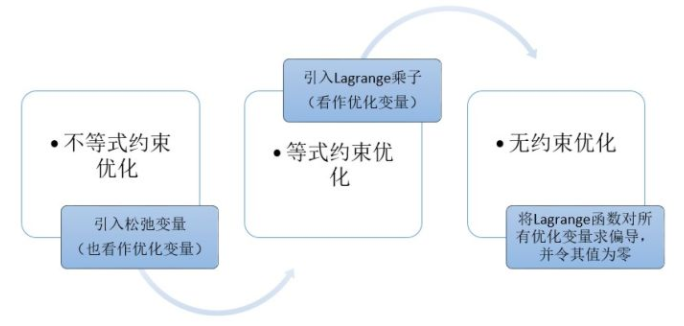
至此，梳理完毕。