【图形学手记】law of the unconscious statistician

以扔色子为例，结果集为{1，2，3，4，5，6}，每个数字出现的概率为1/6

以色子结果为随机变量X，如果我们定义函数F(X) = (X-3)²，我们来计算F(X)的概率分布：

X=1,F(1)=(1−3)2=4,

X=2,F(2)=(2−3)2=1,

X=3,F(3)=(3−3)2=0,

X=4,F(4)=(4−3)2=1,

X=5,F(5)=(5−3)2=4,

X=6,F(6)=(6−3)2=9.

也就是：

Pr(F(0)) = 1/6

Pr(F(1)) = 2/6

Pr(F(4)) = 2/6

Pr(F(9)) = 1/6

如果我们想要算F(X)的期望值，且已经获知了F(X)的概率分布函数，则

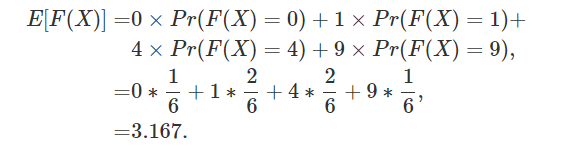
如果记F(X)为随机变量Y，它的概率分布函数记为P_Y，则上式可以写为

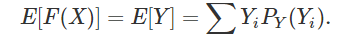
如果我们想要算F(X)的期望值，但不知道F(X)的概率分布函数，我们也可以根据F(X)来进行推算

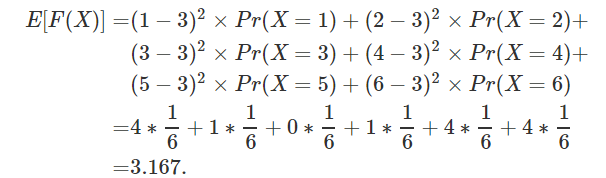
即：

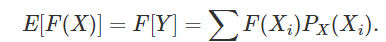
这就是无意识统计学家法则，完整的数学表达如下