LeetCode10 Indexed tree

Binary Indexed Tree（Fenwick tree）：

是一个查询和修改复杂度都为log(n)的数据结构。主要用于查询任意两位之间的所有元素之和，但是每次只能修改一个元素的值；经过简单修改可以在log(n)的复杂度下进行范围修改，但是这时只能查询其中一个元素的值(如果加入多个辅助数组则可以实现区间修改与区间查询)

原理：

树状数组是不需要建树的，通过lowbit来建立一个sum数组(此处为c数组)来维护原来的数组

Lowbit讲解：

c[i]=sum(a[j])  i - lowbit(i) + 1 <= j <= i;

这里的 lowbit(i) 表示将i转换成二进制后的最右边的1到最后所形成的十进制的数。

例如 lowbit(6)=lowbit(110)2=(10)2=2

所以 c[6]=a[5]+a[6];

lowbit(4)=lowbit(100)2=(100)2=4

c[4]=a[1]+a[2]+a[3]+a[4]

lowbit[5]=lowbit(101) 2 =(1) 2=1;

c[5]=a[5]

Lowbit公式：

• lowbit(i)=i&(-i);

公式原理：

上面这个公式是非常重要的，就是通过求出一个数的 Lowbit 将这些数据建立成一个树的，父子节点和线段树关系类似，都是通过某种固定的方式建立起来的。而 lowbit 的原理就是利用了计算机里面的反码和补码（这世界本来就是二进制的！）

我们都知道在计算机中数使用二进制存储的，int 是 4 字节，例如我们把5换成二进制。 5=00000000 00000000 00000000 00000101 这同时也是5的原码。 原码：一个正数，按照值大小转换成的二进制数；一个负数按照绝对值大小转换成的二进制数，然后最高位补1，称为原码。

那么-5的原码就是 -5=10000000 00000000 00000000 00000101 ，其中，最高位的1是符号位。 在计算机中储存一个数用的是补码的形式，要了解补码需要先知道什么是反码。 反码：正数的反码与原码相同，负数的反码为对该数的原码除符号位外各位取反 -5的反码就是： 11111111 11111111 11111111 11111010

再说补码：正数的补码与原码相同，负数的补码是这个数的反码+1 -5：11111111 11111111 11111111 11111010+1= 11111111 11111111 11111111 11111011

那么我们利用这个公式 x&(-x) 的意义：

6&(-6):

6:  00000000 00000000 00000000 00000110

-6:  11111111 11111111 11111111 11111010

Ans:  00000000 00000000 00000000 00000010

所以说 lowbit(6) 的结果很明显就是2

节点i的父亲节点为i+lowbit(i) 若需改变a[i]，则c[i]、c[i+lowbit(i)]、 c[i+lowbit(i)+lowbit(i+lowbit(i)]……一直加到上限，就是需要改变的c数组中的元素。

若需查询s[i]，则 c[i] 、 c[i-lowbit(i)] 、c[i-lowbit(i)-lowbit(i-lowbit(i))] ……就是需要累加的c数组中的元素。 这样我们就让复杂度优化到了 O(logn)

public void change(int index, int val){
    while (index <= maxValue){
        sum[index] += val;
        index += index & (- index);
    }
}

public int sum(int index){
    int sum = 0;
    while( index >= 0){
        sum += sum[index];
        index -= index  & (-index);
    }
}

树状数组原理图：

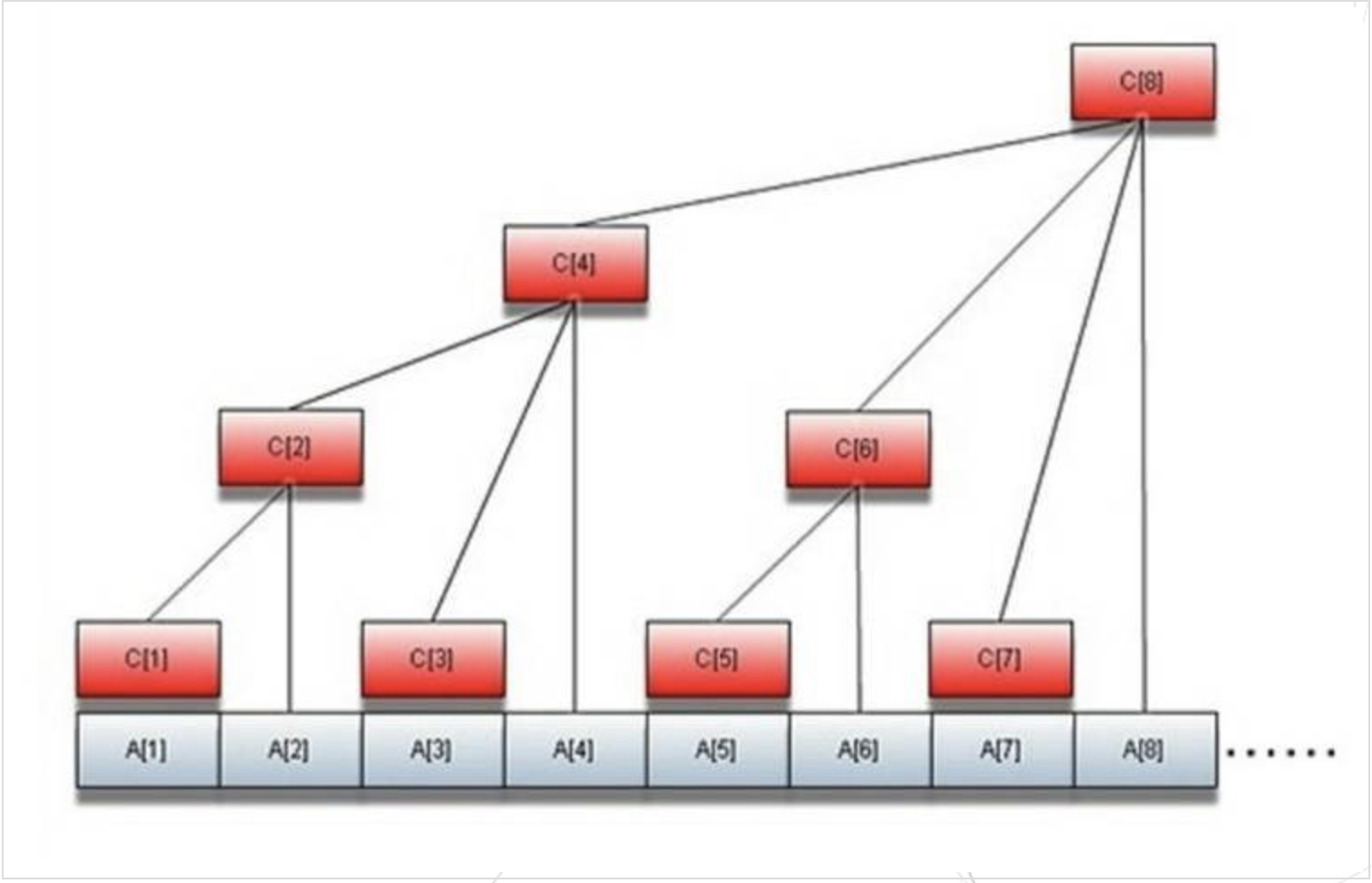
herf: http://xorex.top/2017/05/20/二叉索引树-树状数组-——讲解/

---

2D Binary Indexed Tree (Fenwick Tree)

Algorithm:

We consider the below example. Suppose we have to find the sum of all numbers inside the highlighted area-

We assume the origin of the matrix at the bottom – O.Then a 2D BIT exploits the fact that-

Sum under the marked area = Sum(OB) - Sum(OD) - Sum(OA) + Sum(OC) 

In our program, we use the getSum(x, y) function which finds the sum of the matrix from (0, 0) to (x, y).
Hence the below formula :Sum under the marked area = Sum(OB) - Sum(OD) - Sum(OA) + Sum(OC)

The above formula gets reduced to,
Query(x1,y1,x2,y2) = getSum(x2, y2) - getSum(x2, y1-1) - getSum(x1-1, y2) + getSum(x1-1, y1-1) ;

---

308. Range Sum Query 2D - Mutable

class NumMatrix {
    int [][] tree;
    int [][] matrix;
    int m;
    int n;
    public NumMatrix(int[][] matrix) {
        if(matrix.length == 0 || matrix[0].length == 0) return;// 先判断，再赋值。因为有可能，matrix.length = 0, 那么matrix[0]就会out index boundary。所以上述顺序也不能改变。
        m = matrix.length;
        n = matrix[0].length;
        tree = new int[m + 1][n + 1];//对应的[m][n]的信息其实是存在[m+1][n+1]中
        this.matrix = new int[m][n];
        for(int i = 0; i < m; ++i){
            for(int j = 0; j < n; ++j){
                update(i, j, matrix[i][j]);
            }
        }
    }

    public void update(int row, int col, int val) {
        if(m == 0 || n == 0) return;
        int update = val - matrix[row][col];
        matrix[row][col] = val;//必须要新立一个matrix，因为input只是一个variable，需要一个成员变量来保存
        for(int i = row + 1; i <= m; i += i & (-i)){
            for(int j = col + 1; j <= n; j += j & (-j)){
                tree[i][j] += update;
            }
        }
    }

    public int sumRegion(int row1, int col1, int row2, int col2) {
        if(m == 0 || n == 0) return 0;
        return sum(row2 + 1, col2 + 1) + sum(row1, col1) - sum(row1, col2 + 1) - sum(row2 + 1, col1);
    }

    public int sum(int row, int col){
        int sum = 0;
        for(int i = row; i > 0; i -= i & (-i)){
            for(int j = col; j > 0; j -= j & (-j)){
                sum += tree[i][j];
            }
        }
        return sum;
    }
}

• Time Complexity :
  • Both update and sumRegion function takes O(log(MN)) time.
  • Building the 2D tree takes O(NM log(NM))
  • Answering Q queries takes O(Qlog(NM))
  • M = matrix.length N = matrix[0].length