积分从入门到放弃<2>

这部分重新从定积分学了

1,lnx 的导数就是x^(-1) = 1/x

那么求∫(1/x)dx = ln|x|+C

 2,初值问题.就是求∫f(x)dx = F(x) + C 求C

.

3,Houdini体积映射:

#define PI 3.1415926

vector gmin ;
vector gmax ;
getbbox(,gmin,gmax);

// get sphere radius
float R = gmax.x - gmin.x;
//printf("gmax.x / gmaxmin : %f,%f \n", gmax.x, gmin.x);
float r = R / 2.000f;

vector center = (gmax + gmin)/;
int segments = ;
float dx = R / segments;

function float cylinder_volume(float r ; float h)
{
    return PI * r *r * h;
}

float v = 0.0f;
for(int i=;i<segments;i++)
{
    float ci = lerp(-r, r ,1.0f/segments * i);
    float cylinder_r = sqrt(r*r - ci*ci);
    //printf("r/ci/cylinder_r %f/%f/%f \n" ,r, ci , cylinder_r);
    float cl_volume = cylinder_volume(cylinder_r, dx);
    v += cl_volume;
}
//printf("volume is %f \n" , v);
setdetailattrib(geoself(),"volume",v);

下图可以看到体积小的是黑色.虽然方法积的是圆柱形，最终为球，为了学习积分，没用球的方程

两条曲线之间的面积:

A = ∫ [f(x)-g(x) ] dx  积分上限b,下限a

数值积分: 

有时候不知道反导数怎么求？梯形法，simpson法

曲线积分:求曲线长度:

求普通曲线的长度:

L = ∫ [sqrt(1+dx/dy)^2 ] dy 或者 L=∫ [sqrt(1+dy/dx)^2] dx

求参数方程如图:

x= cos^3t

y = sin^3t

0<= t <= 2π

解方法就是:

√ [(dx/dt)^2 + (dy/dt)^2]

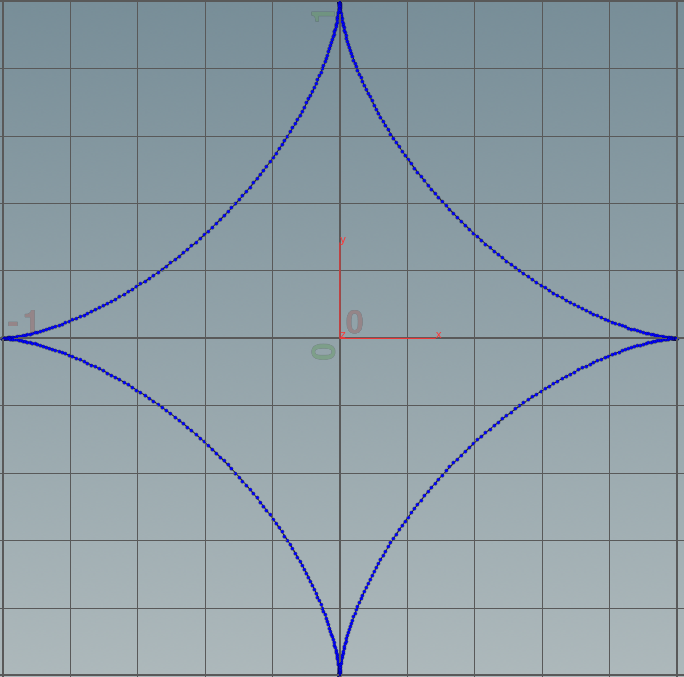
float pi = 3.141596;
float t = fit(@ptnum,,@numpt-,,) *  * pi;
@P.x = cos(t) * cos(t) * cos(t);
@P.y = sin(t) * sin(t) * sin(t);

HoudiniCode

蒙特卡洛求PI

曲线下的面积/矩形面积 = 曲线下的总点数/随机点的总数

<1>求PI

import random,math

import numpy as np
import matplotlib.pyplot as plt

N = 100000
distance = lambda x, y: math.sqrt(x * x + y * y)

np.random.seed(100)
x = np.random.uniform(-1,1,N)
np.random.seed(200)
y = np.random.uniform(-1,1,N)

def Monte_carlo_PI():
    hitNum = 0
    for index in xrange(0,N,1):
        if distance(x[index],y[index]) <=1 :
            hitNum += 1
    proportion_seed = float(hitNum)/float(N)
    return proportion_seed * 4

if __name__ == "__main__":
    print Monte_carlo_PI()

    fig = plt.figure(figsize=(10,10))

    ax = fig.add_subplot(111)
    ax.spines['top'].set_color('none')
    ax.spines['right'].set_color('none')
    ax.xaxis.set_ticks_position('bottom')
    ax.spines['bottom'].set_position(('data', 0))
    ax.yaxis.set_ticks_position('left')
    ax.spines['left'].set_position(('data', 0))

    #plt.plot(xs,ys,'r')
    #plt.scatter(0, 0, s=100000)
    circle2 = plt.Circle((0, 0), 1, color='r',alpha = 0.5)
    ax.add_patch(circle2)

    plt.scatter(x, y,s=1,c="black")
    plt.grid(True)
    plt.show()

python_mente_claro

功:

弹簧做功:弹簧的积分区域一定是变化了多少，从0开始积分变化了多少。如下

1,弹簧系数: 把弹簧从自然长度2米拉到5米做功为1800焦耳,求弹簧的弹力系数.

弹簧力是:F = kx (系数*变化的距离)

弹簧做功:∫F(x)dx  积分阈为[0,变化长度]

所以W ∫F(x)dx = k/2 * x^2    [0,3]

W(3) - W(0) = 1800 ,k = 400牛顿/米

抽水做功:

第一步(薄片体积)        :       ΔV = PI * r^2  Δy                  这里薄片体积表示为圆柱

第二步(薄片力)            :      F(y) = ΔV * 比重

第三步(薄片需要的功)   :    ΔW = 力 X 力的作用距离 = F(y) *   (距离-y)

第四步(黎曼和总功)      :    w =Σ ΔW

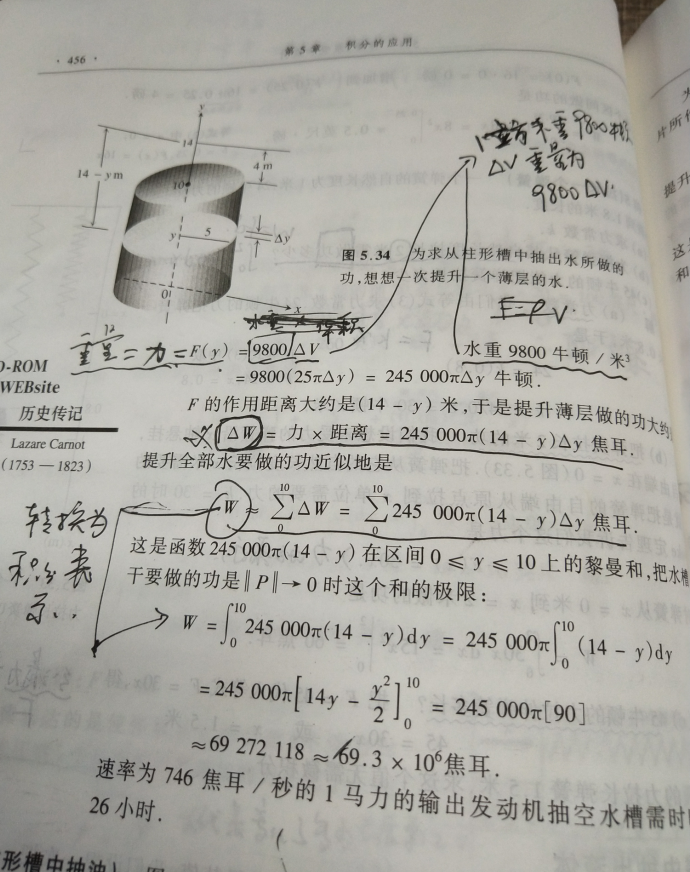
矩和质心

....