P1579哥德巴赫猜想

写来自己学习用~

题目内容：

1742年6月7日哥德巴赫写信给当时的大数学家欧拉，正式提出了以下的猜想：任何一个大于9的奇数都可以表示成3个质数之和。质数是指除了1和本身之外没有其他约数的数，如2和11都是质数，而6不是质数，因为6除了约数1和6之外还有约数2和3。需要特别说明的是1不是质数。

现在请你编一个程序验证哥德巴赫猜想。

先给出一个奇数n，要求输出3个质数，这3个质数之和等于输入的奇数。

输入格式：

仅有一行，包含一个正奇数n，其中9<n<20000

输出格式：

仅有一行，输出3个质数，这3个质数之和等于输入的奇数。相邻两个质数之间用一个空格隔开，最后一个质数后面没有空格。如果表示方法不唯一，请输出第一个质数最小的方案，如果第一个质数最小的方案不唯一，请输出第一个质数最小的同时，第二个质数最小的方案。

方法：

在入门题目里面，所以首先觉得暴力应该能过，但是有两组数据超时了。

于是想到之前做的求一百亿以内的素数那道题（最初一直在用筛法），所以在做这道题是就先根据素数的倍数一定不是素数，对n以内所有非素数进行标记，在后面的程序中就不需要用函数判断是否是素数了。

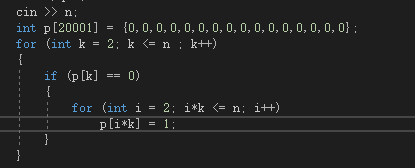
之后就直接做就可以了。