prim算法和克鲁斯卡尔算法

Prim

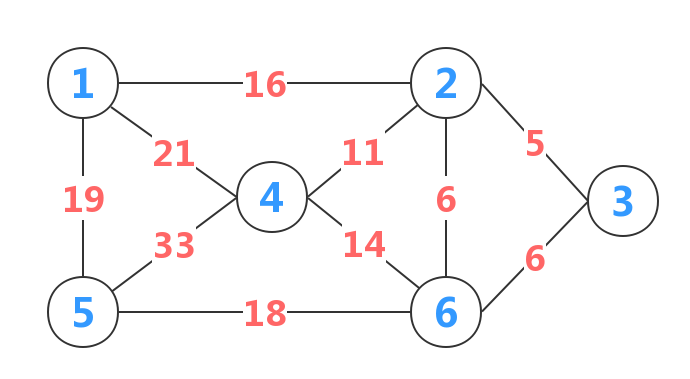
设图G=(V,E)是一个具有n个顶点的连通网，其生成树的顶点集合为U。首先把v0放入U，再在所有的u∈U,v∈V-U的边(u,v)∈E中找一条最小权值的边，加入生成树，并把该边的v加入U集合。如果U集合已经有n个元素，则结束，否则在剩下的部分中继续寻找最小权值的边。

 #include<stdio.h>
 #include<stdlib.h>

 #define infinity 9999
 #define MAX 20

 int G[MAX][MAX],spanning[MAX][MAX],n;

 int prims();

 int main()
 {
     int i,j,total_cost;
     printf("Enter no. of vertices:");
     scanf("%d",&n);

     printf("\nEnter the adjacency matrix:\n");

     for(i=;i<n;i++)
         for(j=;j<n;j++)
             scanf("%d",&G[i][j]);

     total_cost=prims();
     printf("\nspanning tree matrix:\n");

     for(i=;i<n;i++)
     {
         printf("\n");
         for(j=;j<n;j++)
             printf("%d\t",spanning[i][j]);
     }

     printf("\n\nTotal cost of spanning tree=%d",total_cost);
     return ;
 }

 int prims()
 {
     int cost[MAX][MAX];
     int u,v,min_distance,distance[MAX],from[MAX];
     int visited[MAX],no_of_edges,i,min_cost,j;

     //create cost[][] matrix,spanning[][]
     for(i=;i<n;i++)
         for(j=;j<n;j++)
         {
             if(G[i][j]==)
                 cost[i][j]=infinity;
             else
                 cost[i][j]=G[i][j];
                 spanning[i][j]=;
         }

     //initialise visited[],distance[] and from[]
     distance[]=;
     visited[]=;

     for(i=;i<n;i++)
     {
         distance[i]=cost[][i];
         from[i]=;
         visited[i]=;
     }

     min_cost=;        //cost of spanning tree
     no_of_edges=n-;        //no. of edges to be added

     while(no_of_edges>)
     {
         //find the vertex at minimum distance from the tree
         min_distance=infinity;
         for(i=;i<n;i++)
             if(visited[i]==&&distance[i]<min_distance)
             {
                 v=i;
                 min_distance=distance[i];
             }

         u=from[v];

         //insert the edge in spanning tree
         spanning[u][v]=distance[v];
         spanning[v][u]=distance[v];
         no_of_edges--;
         visited[v]=;

         //updated the distance[] array
         for(i=;i<n;i++)
             if(visited[i]==&&cost[i][v]<distance[i])
             {
                 distance[i]=cost[i][v];
                 from[i]=v;
             }

         min_cost=min_cost+cost[u][v];
     }

     return(min_cost);
 }

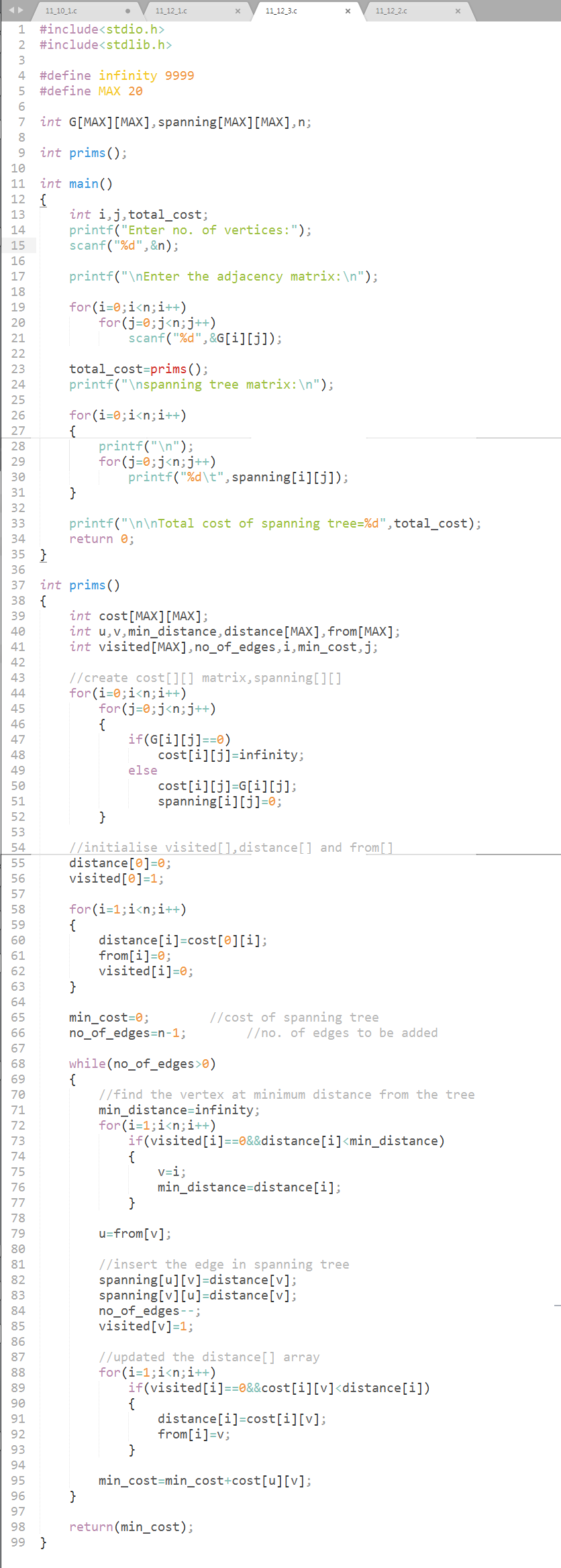
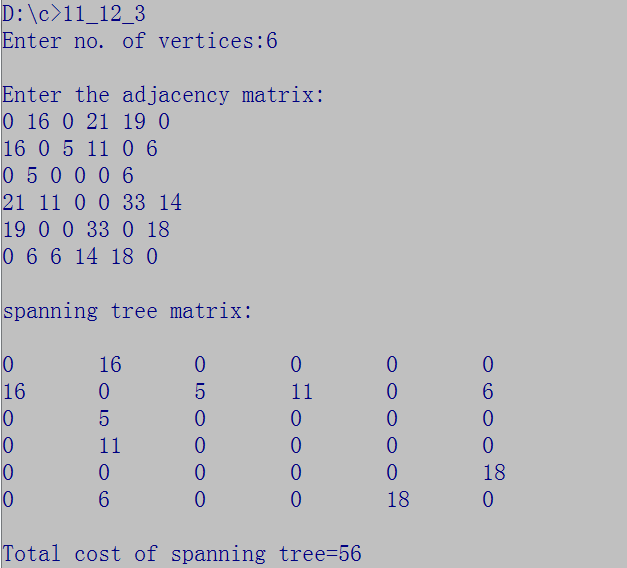
COST = 16 + 5 + 6 + 11 + 18 =

Kruskal

 #include<stdio.h>

 #define MAX 30

 typedef struct edge
 {
     int u,v,w;
 }edge;

 typedef struct edgelist
 {
     edge data[MAX];
     int n;
 }edgelist;

 edgelist elist;

 int G[MAX][MAX],n;
 edgelist spanlist;

 void kruskal();
 int find(int belongs[],int vertexno);
 void union1(int belongs[],int c1,int c2);
 void sort();
 void print();

 void main()
 {
     int i,j,total_cost;

     printf("\nEnter number of vertices:");

     scanf("%d",&n);

     printf("\nEnter the adjacency matrix:\n");

     for(i=;i<n;i++)
         for(j=;j<n;j++)
             scanf("%d",&G[i][j]);

     kruskal();
     print();
 }

 void kruskal()
 {
     int belongs[MAX],i,j,cno1,cno2;
     elist.n=;

     for(i=;i<n;i++)
         for(j=;j<i;j++)
         {
             if(G[i][j]!=)
             {
                 elist.data[elist.n].u=i;
                 elist.data[elist.n].v=j;
                 elist.data[elist.n].w=G[i][j];
                 elist.n++;
             }
         }

     sort();

     for(i=;i<n;i++)
         belongs[i]=i;

     spanlist.n=;

     for(i=;i<elist.n;i++)
     {
         cno1=find(belongs,elist.data[i].u);
         cno2=find(belongs,elist.data[i].v);

         if(cno1!=cno2)
         {
             spanlist.data[spanlist.n]=elist.data[i];
             spanlist.n=spanlist.n+;
             union1(belongs,cno1,cno2);
         }
     }
 }

 int find(int belongs[],int vertexno)
 {
     return(belongs[vertexno]);
 }

 void union1(int belongs[],int c1,int c2)
 {
     int i;

     for(i=;i<n;i++)
         if(belongs[i]==c2)
             belongs[i]=c1;
 }

 void sort()
 {
     int i,j;
     edge temp;

     for(i=;i<elist.n;i++)
         for(j=;j<elist.n-;j++)
             if(elist.data[j].w>elist.data[j+].w)
             {
                 temp=elist.data[j];
                 elist.data[j]=elist.data[j+];
                 elist.data[j+]=temp;
             }
 }

 void print()
 {
     int i,cost=;

     for(i=;i<spanlist.n;i++)
     {
         printf("\n%d\t%d\t%d",spanlist.data[i].u,spanlist.data[i].v,spanlist.data[i].w);
         cost=cost+spanlist.data[i].w;
     }

     printf("\n\nCost of the spanning tree=%d",cost);
 }