PID控制器开发笔记之二：积分分离PID控制器的实现

前面的文章中，我们已经讲述了PID控制器的实现，包括位置型PID控制器和增量型PID控制器。但这个实现只是最基本的实现，并没有考虑任何的干扰情况。在本节及后续的一些章节，我们就来讨论一下经典PID控制器的优化与改进。这一节我们首先来讨论针对积分项的积分分离优化算法。

1、基本思想

我们已经讲述了PID控制引入积分主要是为了消除静差，提高控制精度。但在过程的启动、结束或大幅度增减设定值时，短时间内系统输出有很大偏差，会造成PID运算的积分累积，引起超调或者振荡。为了解决这一干扰，人们引入了积分分离的思想。其思路是偏差值较大时，取消积分作用，以免于超调量增大；而偏差值较小时，引入积分作用，以便消除静差，提高控制精度。

具体的实现步骤是：根据实际情况，设定一个阈值；当偏差大于阈值时，消除积分仅用PD控制；当偏差小于等于阈值时，引入积分采用PID控制。则控制算法可表示为：

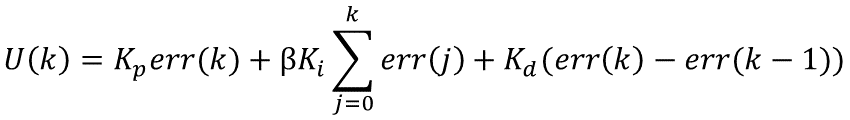
其中β称为积分开关系数，其取值范围为：

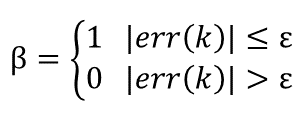
由上述表述及公式我们可以知道，积分分离算法的效果其实与ε值的选取有莫大关系，所以ε值的选取实际上是实现的难点，ε值过大则达不到积分分离的效果，而ε值过小则难以进入积分区，ε值的选取存在很大的主观因素。

对于经典的增量式PID算法，似乎没有办法由以上的公式推导而来，因为β随着err(k)的变化在不是修改着控制器的表达式。其实我们可以换一种角度考虑，每次系统调节未定后，偏差应该为零，然后只有当设定值改变时，系统才会响应而开始调节。设定值的改变实际上是一个阶跃变化，此时的控制输出记为U₀，开始调节时，其调节增量其实与之前的一切没有关系。所以我们就可以以变化时刻开始为起点，而得到带积分分离的增量算法，以保证在启动、停止和快速变化时防止超调。公式如下：

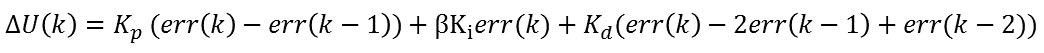
其中β的取值与位置型PID算法一致。可能有人会担心偏差来回变化，造成积分作用的频繁分离和引入，进而使上述的增量表达式无法实现。其实我们分析一下就能发现，在开始时，由于设定值变化引起的偏差大而分离了积分作用，在接近设定值时，偏差变小就引入了积分，一边消除静差，而后处于稳态，直到下一次变化。

2、算法实现

这一部分，我们根据前面对其基本思想的描述，来实现基于积分分离的PID算法实现，同样是包括位置型和增量型两种实现方式。首先我们来看一下算法的实现过程，具体的流程图如下：

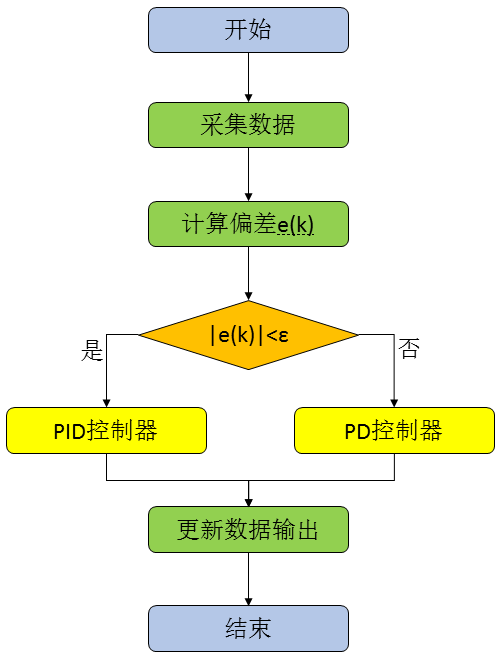
有上图我们知道，与普通的PID算法的区别，只是判断偏差的大小，偏差大时，为PD算法，偏差小时为PID算法。于是我们需要一个偏差检测与积分项分离系数β的函数。

 static uint16_t BetaGeneration(float error,float epsilon)

 {

   uint16_t beta=;

   if(abs(error)<= epsilon)

 {

   beta=;

 }

 return beta;

 }

（1）位置型PID算法实现

根据前面的分析我们可以很轻松的编写程序，只需要在编写程序时判断偏差以确定是否引入积分项就可以了。同样先定义PID对象的结构体：

 /*定义结构体和公用体*/

 typedef struct

 {

   float setpoint;       //设定值

   float proportiongain;     //比例系数

   float integralgain;      //积分系数

   float derivativegain;    //微分系数

   float lasterror;     //前一拍偏差

   float result; //输出值

   float integral;//积分值

   float epsilon; //偏差检测阈值

 }PID;

接下来实现PID控制器：

 void PIDRegulation(PID *vPID, float processValue)

 {

   float thisError;

   thisError=vPID->setpoint-processValue;

   vPID->integral+=thisError;

   uint16_t beta= BetaGeneration(error, vPID->epsilon);

   if(beta>)

 {

   vPID->result=vPID->proportiongain*thisError+vPID->derivativegain*(thisError-vPID->lasterror);

 }

 else

 {

 vPID->result=vPID->proportiongain*thisError+vPID->integralgain*vPID->integral+vPID->derivativegain*(thisError-vPID->lasterror);

 }

   vPID->lasterror=thisError;

 }

与普通的PID算法的区别就是上述代码中增加了偏差判断，来决定积分项的分离与否。

（2）增量型PID算法实现

对于增量型PID控制，我们也可以采取相同的处理。首先定义PID对象的结构体：

 /*定义结构体和公用体*/

 typedef struct

 {

   float setpoint;       //设定值

   float proportiongain;     //比例系数

   float integralgain;      //积分系数

   float derivativegain;    //微分系数

   float lasterror;     //前一拍偏差

   float preerror;     //前两拍偏差

   float deadband;     //死区

   float result; //输出值

   float epsilon; //偏差检测阈值

 }PID;

接下来实现PID控制器：

 void PIDRegulation(PID *vPID, float processValue)

 {

   float thisError;

   float increment;

   float pError,dError,iError;

   thisError=vPID->setpoint-processValue; //得到偏差值

   pError=thisError-vPID->lasterror;

   iError=thisError;

   dError=thisError-*(vPID->lasterror)+vPID->preerror;

   uint16_t beta= BetaGeneration(error, vPID->epsilon);

   if(beta>)

 {

 increment=vPID->proportiongain*pError+vPID->derivativegain*dError;   //增量计算

 }

 else

 {

 increment=vPID->proportiongain*pError+vPID->integralgain*iError+vPID->derivativegain*dError;   //增量计算

 }

   vPID->preerror=vPID->lasterror;  //存放偏差用于下次运算

   vPID->lasterror=thisError;

   vPID->result+=increment;

 }

这就实现了增量型PID控制器积分分离算法，也没有考虑任何的干扰条件，仅仅只是对数学公式的计算机语言化。

3、总结

积分分离算法的思想非常简单。当然，对于β的取值，很多人提出了改进措施，例如分多段取值，设定多个阈值ε₁、ε₂、ε₃、ε₄等，不过这些阈值也需要根据实际的系统来设定。除了分段取值外，甚至也有采用函数关系来获取β值。当然，这样处理后就不再是简单的积分分离了，特别是在增量型算法中，实际上已经演变为一种变积分算法了。已经偏离了积分分离算法的设计思想，在后面我们会进一步说明。

欢迎关注：