Randomized Online PCA Algorithms with Regret Bounds that are Logarithmic in the Dimension

Setup of Batch PCA and Online PCA
Hedge Algorithm
改进算法
用于矩阵
$rounding()$

前俩次，都用到了$rounding()$,遗憾的是，都没有讲清楚，这次稍微具体地讲下这篇论文。但是说实话，我感觉，我还是没有领会到这篇文章的精髓。

Setup of Batch PCA and Online PCA

Batch PCA的目标，就是寻找一个子空间，能够最小化平方误差。
这篇论文，给出了一个比较新颖的表达方式：

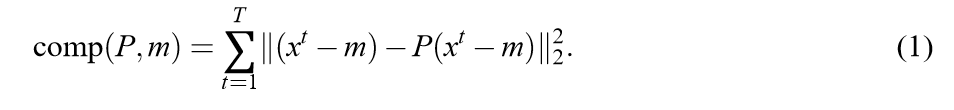
where,
$m\in \mathbb{R}^{n}$
$rank(P) =k$
一般来讲，最优解就是，$m = \overline{x}$, 而$P$所对应的子空间就是协方差矩阵的前$k$个特征向量组成的子空间。
论文对（1）进行了一个改写：

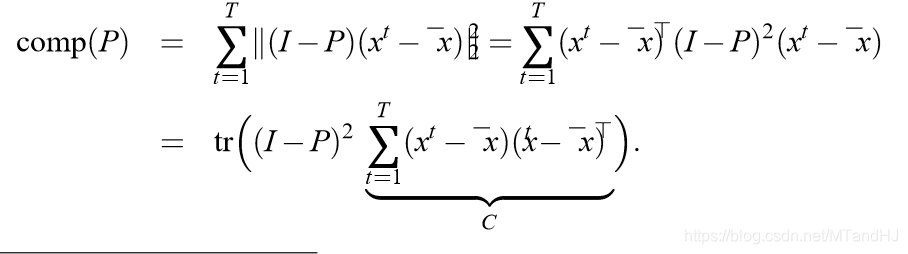
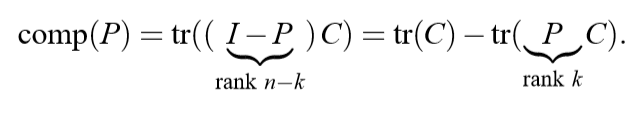
上面式子的一种直观解释就是，$comp(P)$就是一种损失，这个损失是由投影矩阵$P$带来的。
而在streaming PCA(论文里为Online PCA):

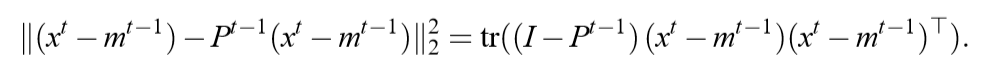
很自然的，

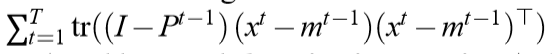
成了$T$次迭代所积累的损失。
我们希望，这些损失，能够接近由Batch PCA所产生的损失。

Hedge Algorithm

假设，有$n$个专家:expert $i$, $i=1,2,\ldots,n$.
有一个概率向量$\mathsf{w}$,每个元素$\mathsf{w}_i$为舍弃expert $i$的概率。
自然而然，会有一个损失，称之为:$\mathcal{l}$,每个元素是舍弃相应expert的损失，但是要求$\mathcal{l}\in[0,1]$，所以我估计得有个单位化的过程。
下面就是如何选取专家，和迭代更新$\mathsf{w}$的算法。

这个$\mathbf{w}$的更新，有点类似adaboost，感觉其它地方也有看到过，至于其中的原理，估计还是得看论文吧。
同时，有下面的性质：

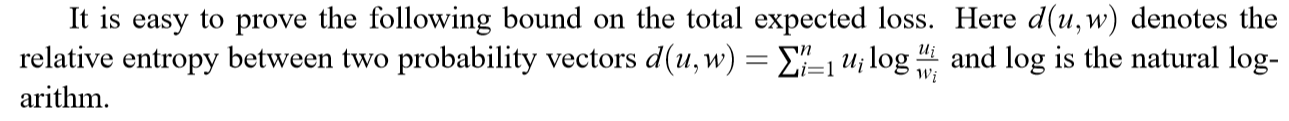
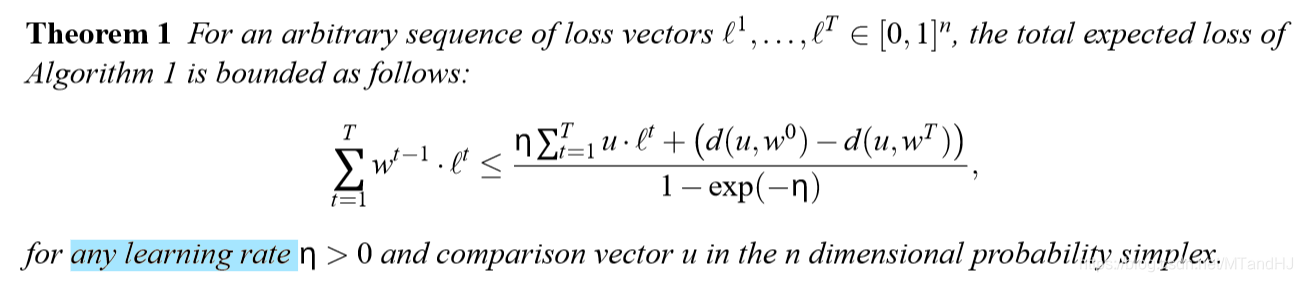
改进算法

这个算法的目标是，将$\mathbf{w}$分解为$\mathop{\sum}\limits_{i}p_ir_i$,其中$p_i$为概率,$r_i$为$(n-k)$-corner.$d$-corner,是指有且仅有$d$个非零项，且非零项的值为：$\frac{1}{d}$.分解完毕只有，不同于上面的算法，这个算法将通过分布$p_i$选择$r_i$,而$r_i$中的非零项所对应的指标就是相应的要舍弃的专家，expert。
分解算法如下：

$\mathbf{w} \in B_d^n$是指$|\mathbf{w}|=\mathop{\sum}\limits_{i}\mathbf{w}_i=1$,且$0 \leq \mathbf{w}_i \leq \frac{1}{d}$

为了使$\mathbf{w} \in B_d^{n}$,有下面的算法:

接下来就是结合上面的分解所得到的改进的Hedge算法：

有一个性质:

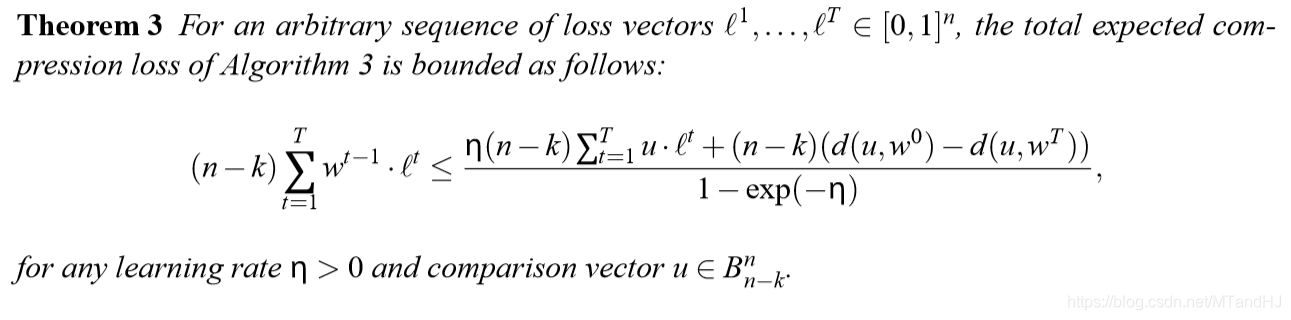
用于矩阵

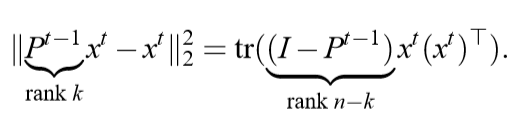
定义：

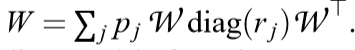
矩阵$d$-corner是指$A$的特征值，有且仅有$d$个非零项，且均为$\frac{1}{d}$。
其他的类似定义。
这里的$W$是密度矩阵：对称正定矩阵，且迹为1。
则：

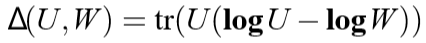
$\mathbf{log}A=\mathop{\sum}\limits_ilog(\lambda_i)a_ia_i^{\top}$, 如果$A=\mathop{\sum}\limits_i\lambda_ia_ia_i^{\top}$
$\mathbf{exp}A$同理。

这个算法貌似是为了将$W$投影到$B_d^{n}$中的理论依据。

下面的算法五，就是关于如何利用$W$进行PCA：

$rounding()$

那么如何将上面的种种算法应用到之前提到的文章呢。之前的文章说，算法二就可以了，所以是这么理解吗？
最后得到的矩阵，根据特征值，得到概率向量$\mathbf{w}$，然后再进行分解，通过概率$p_i$，得到$r_i$，接着，舍弃这些特征向量，得到最后的投影矩阵$P$?
但是，用特征值，总觉得和上面的不大相符，可不用特征值又能用什么呢？因为他们都是在最后一步利用这个$rounding()$。但是，用算法五，就和他们本身的算法不一致了，具体如何，不得而知了。