机器学习---感知机（Machine Learning Perceptron）

感知机（perceptron）是一种线性分类模型，通常用于二分类问题。感知机由Rosenblatt在1957年提出，是神经网络和支持向量机的基础。通过修改损失函数，它可以发展成支持向量机；通过多层堆叠，它可以发展成神经网络。因此，虽然现在已经不再广泛使用感知机模型了，但是了解它的原理还是有必要的。

先来举一个简单的例子。比如我们可以通过某个同学的智商和学习时间（特征）来预测其某一次的考试成绩（目标），如果考试成绩在60分以上即为及格，在60分以下为不及格。这和线性回归类似，只不过设定了一个阈值，使得其可以处理分类问题。

因此，我们定义：给定特征向量x=([x₁,x₂,...,x_n])^T以及每个特征的权重w=([w₁,w₂,...,w_n])^T，目标y共有正负两类。那么：

对于某个样本，如果其 wx > 阈值（threshold），那么将其分类到正类，记为y=+1；

如果其 wx < 阈值（threshold），那么将其分类到负类，记为y=-1；

（注：wx是特征向量和权重向量的点积/内积，wx=w₁x₁+w₂x₂+...+w_nx_n）

也就是说，上式分为两种情况：wx - 阈值（threshold）> 0 或 wx - 阈值（threshold）< 0。我们可以将目标方程式简写成：f(x)=sign(wx+b)。

（注：sign是符号函数）

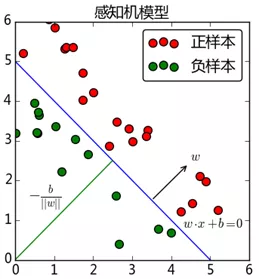
wx+b=0对应于特征空间中的一个超平面，用来分隔两个类别，其中w是超平面的法向量，b是超平面的截距。

为了便于叙述，把b并入权重向量w，记作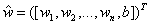，特征向量则扩充为。这样我们可以把目标方程式写成：。（为了简便的缘故，下面还是都写成f(x)=sign(wx)）

我们希望能找出这样一个超平面（当然在二维空间是找到一条直线），使得所有样本都能分类正确。那么应该怎么做呢？一个自然的想法就是先随意初始化一个超平面，如果出现分类错误的现象，那么我们再将原来的这个超平面进行修正，直至所有样本分类正确。从一定程度上讲，人类就是如此进行学习的，发现错误即改正，所以说感知机是一个知错能改的模型。

错误分为两种情况：

一种情况是错误地将正样本（y=+1）分类为负样本（y=-1）。此时，wx<0，即w与x的夹角大于90度，因此修正的方法是让夹角变小，可以把w向量减去x向量，也就是将w修正为w+yx。

另一种情况是错误地将负样本（y=-1）分类为正样本（y=+1）。此时，wx>0，即w与x的夹角小于90度，因此修正的方法是让夹角变大，可以把w向量加上x向量，也就是将w修正为w+yx。

    

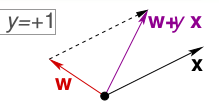
可以看到，这两种情况下修正的方式都是相同的，因此，我们可以通过不断迭代，最终使超平面做到完全分类正确。我们将PLA（Perceptron Linear Algorithm，即线性感知机算法）简单总结如下：

1，初始化w

2，找出一个分类错误点

3，修正错误，假设迭代次数为t次（t=0,1,...），那么修正公式为：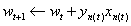

4，直至没有分类错误点，返回最终的w

下面是台湾大学林轩田老师在《Machine Learning Foundation》中提到的示例，用来说明感知机算法。

首先，用原点到x₁点的向量作为w_t的初始值。

分类平面与w_t垂直，可以看到，有一个点x₃被分类错误，本来是正类，却被分到了负类，因此我们需要使w_t与x₃之间的夹角变小，w_t更新为w_t+1。

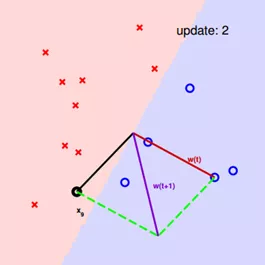
不断修正，直至完全分类正确。

从另一个角度来看，我们只要确定了参数w，也就可以找到这个分离超平面。和其他机器学习模型类似，我们首先定义损失函数，然后转化为最优化问题，可以用梯度下降等方法不断迭代，最终学习到模型的参数w。

我们很自然的会想到用错误分类点的总数来作为损失函数，也就是，但是根据林轩田老师所说，这是一个NP Hard问题，是无法解决的。

既然不能用错误分类点的总数作为损失函数，那么只能寻找其它表现形式。感知机算法选择所有错误分类点距离分离超平面的总距离作为损失函数，也就是要让错误分类点距离超平面的总长度最小。

这个总长度是怎么来的呢？

首先，输入空间Rⁿ中任意一点x₀到超平面S的距离为：

 

对于错误分类点（x_i，y_i）来说：

 

因此，错误分类点x_i到超平面S的距离可以写成：

 

假设超平面的错误分类点的集合为M，那么所有的错误分类点到超平面S的总距离为：

 

不考虑 ||w|| ，就得到感知机学习的损失函数：

（注：为什么不考虑 ||w|| ？因为感知机算法最终并不关心超平面离各点的距离有多少，只是关心最后是否已经完全分类正确，所以在最后才可以不考虑||w||。）

 

然后就是使用随机梯度下降法（SGD）不断极小化损失函数。损失函数L（w,b）的梯度由以下式子给出（对w，b分别求偏导）：

 

随机选取一个误分类点（x_i，y_i），对w，b进行更新：

 

直至超平面能够完全分类正确，返回w，b。这和上面说的方法其实是一样的。

 

算法看起来很简单是吧？但是还有几个小细节我们需要考虑。

• 分离超平面是否只有一个？显然，如果我们把上面示例里的这个平面稍微倾斜一点，新的平面也还是可以完全分类正确的。也就是说，感知机算法的解不止一个，这主要取决于w初始值和分类错误点的选择。
• 使用感知机算法是否需要满足某种假设？由于感知机算法是线性分类器，因此数据必须线性可分（linear seperable），否则，感知机算法就无法找到一个完全分类正确的超平面，算法会一直迭代下去，不会停止。
• 假如数据满足线性可分这一假设，那么是否经过T次迭代，感知机算法一定能停止呢？也就是说，感知机算法最后是否一定能收敛。答案是会收敛。感知机算法收敛性的证明：http://txshi-mt.com/2017/08/03/NTUML-2-Learning-to-Answer-Yes-No/。
• 我们现在知道感知机算法最终一定会停下来，但是多久会停呢？由于T和目标参数w_f有关，而w_f是未知的，因此我们不知道T最大是多少。

上面讨论的是数据完美线性可分的情况，那么如果数据线性不可分呢？现实中，很多时候都存在两个分类的数据混淆在一起的情况，PLA显然解决不了这样的问题。那么怎么办呢？其实只需把感知机算法稍微修改一下，找到一个犯错最少的超平面即可。具体的做法就是在寻找的过程中把最好的超平面记住（放在口袋里），因此这被称之为口袋算法（Pocket Algorithm）。

Pocket Algorithm简单总结如下：

1，初始化w，把w作为最好的解放入口袋

2，随机找出一个分类错误点

3，修正错误，假设迭代次数为t次（t=0,1,...），那么修正公式为：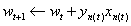

4，如果w_t+1比w犯的错误少，那么用w_t+1替代w

5，经过t次迭代后停止，返回口袋里最终的结果