全排列12 · Permutations

无重复

［抄题］：

Given a collection of numbers, return all possible permutations.

For example,
[1,2,3] have the following permutations:
[1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], and [3,2,1].

［思维问题］：

不知道回溯法：和求子集一样-[1],[1,2]-只剩[1]

123用了2，312又要用2。反复用，所以叫回溯法

［一句话思路］：

［输入量］：空： 正常情况：特大：特小：程序里处理到的特殊情况：异常情况（不合法不合理的输入）：

［画图］：

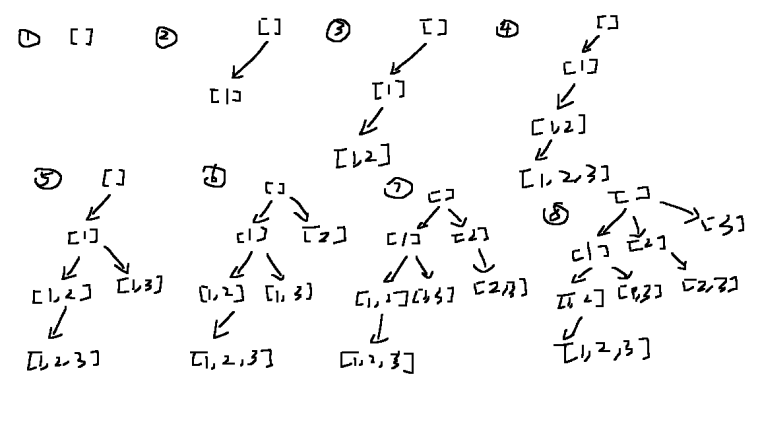
［一刷］：

1. 递归退出用return;表示 递归推出的出口在helper函数中，不在每个点加进permutation的过程中
2. 结果是复数数组，返回results 如果nums == null,返回[] 如果nums.length == 0, 返回[[]](result中添加一个空数组，返回result)
3. ist.size()的效果等于nums.length
4. helper调用整个数组时，参数是数组名

［二刷］：

［三刷］：

［四刷］：

［五刷］：

[五分钟肉眼debug的结果]：

［总结］：

1. 搜索递归的三个步骤：新参数、递归、去掉新参数
2. 不知道回溯法：和求子集一样-[1],[1,2]-只剩[1]

［复杂度］：Time complexity: O() Space complexity: O()

［英文数据结构或算法，为什么不用别的数据结构或算法］：

［其他解法］：

［Follow Up］：

［LC给出的题目变变变］：

public class Solution {
    /*
     * @param nums: A list of integers.
     * @return: A list of permutations.
     */
    public List<List<Integer>> permute(int[] nums) {
        //corner case
        List<List<Integer>> results = new ArrayList<>();
        List<Integer> permutations = new ArrayList<>();
        HashSet<Integer> set = new HashSet<>();

        if (nums == null) {
            return null;
        }
        if (nums.length == 0) {
            //return new ArrayList<>();
            results.add(new ArrayList<>());
            return results;
        }
        //helper
        helper(nums, permutations, set, results);
        //return
        return results;
    }
    //helper
    public void helper (int[] nums, List<Integer> permutations,
    HashSet<Integer> set, List<List<Integer>> results) {
        if (permutations.size() == nums.length) {
            results.add(new ArrayList<>(permutations));
            return ;//
        }

        for (int i = 0; i < nums.length; i++) {
            if (set.contains(nums[i])) {
                continue;
            }
            permutations.add(nums[i]);
            set.add(nums[i]);
            helper(nums, permutations, set, results);
            set.remove(nums[i]);
            permutations.remove(permutations.size() - 1);
        }
    }
}

有重复

［抄题］：

［思维问题］：

有重复元素不知道是默认不排序的，要先排序

［一句话思路］：

排序后用visited数组来控制

［输入量］：空： 正常情况：特大：特小：程序里处理到的特殊情况：异常情况（不合法不合理的输入）：

［画图］：

((i != 0 && visited[i - 1] == 0) &&
nums[i - 1] == nums[i]//
)

在不是第零位（没有前一位）的前提下，如果两数字相同，前面一个数却没有访问，此时不可

［一刷］：

1. 有数组要先排序
2. 设置visited数组默认为0

［二刷］：

［三刷］：

［四刷］：

［五刷］：

[五分钟肉眼debug的结果]：

不要把visited nums数组名写错了

［总结］：

代码风格：太长可以换行、不要用很多的&& ||符号

［复杂度］：Time complexity: O(分支的深度次方) Space complexity: O(深度*分支)

［英文数据结构或算法，为什么不用别的数据结构或算法］：

［其他解法］：

［Follow Up］：

［LC给出的题目变变变］：

31. Next Permutation 如果不是要求找出全部排列的，就几乎都是做数组调整 玩文字游戏

public class Solution {
    /*
     * @param nums: A list of integers.
     * @return: A list of permutations.
     */
    public List<List<Integer>> permuteUnique(int[] nums) {
        //corner case
        List<List<Integer>> results = new ArrayList<>();
        List<Integer> permutations = new ArrayList<>();
        int[] visited = new int[nums.length];

        if (nums == null) {
            return null;
        }
        if (nums.length == 0) {
            results.add(new ArrayList<>());
            return results;
        }
        //helper
        Arrays.sort(nums);
        for (int i = 0; i < nums.length; i++) {
            visited[i] = 0;
        }
        helper(nums, permutations, visited, results);
        //return
        return results;
    }
    //helper
    public void helper (int[] nums, List<Integer> permutations,
    int[] visited, List<List<Integer>> results) {
        if (permutations.size() == nums.length) {
            results.add(new ArrayList<>(permutations));
            return ;//
        }

        for (int i = 0; i < nums.length; i++) {
            if (visited[i] == 1) {
                continue;
            }
            if ((i != 0 && visited[i - 1] == 0) &&
                nums[i - 1] == nums[i]//
            ) {
                continue;
            }
            visited[i] = 1;
            permutations.add(nums[i]);
            helper(nums, permutations, visited, results);
            permutations.remove(permutations.size() - 1);
            visited[i] = 0;
        }
    }
}