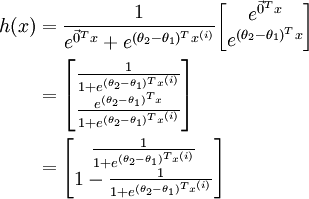
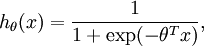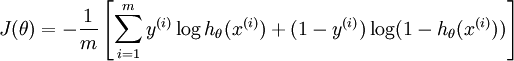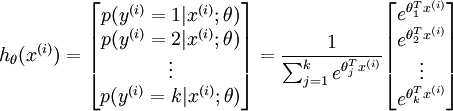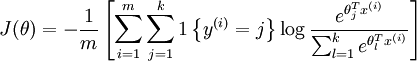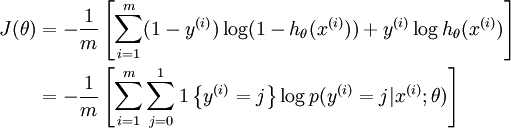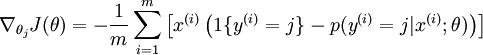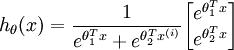【机器学习】Softmax 和Logistic Regression回归Sigmod
二分类问题Sigmod
在 logistic 回归中,我们的训练集由 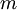 个已标记的样本构成:
个已标记的样本构成: ,其中输入特征
,其中输入特征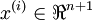 。(我们对符号的约定如下:特征向量
。(我们对符号的约定如下:特征向量  的维度为
的维度为 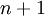 ,其中
,其中 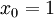 对应截距项 。) 由于 logistic 回归是针对二分类问题的,因此类标记
对应截距项 。) 由于 logistic 回归是针对二分类问题的,因此类标记 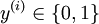 。假设函数(hypothesis function) 如下:
。假设函数(hypothesis function) 如下:
我们将训练模型参数  ,使其能够最小化代价函数 :
,使其能够最小化代价函数 :
多分类问题
在一个多分类问题中,因变量y有k个取值,即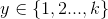 。例如在邮件分类问题中,我们要把邮件分为垃圾邮件、个人邮件、工作邮件3类,目标值y是一个有3个取值的离散值。这是一个多分类问题,二分类模型在这里不太适用。
。例如在邮件分类问题中,我们要把邮件分为垃圾邮件、个人邮件、工作邮件3类,目标值y是一个有3个取值的离散值。这是一个多分类问题,二分类模型在这里不太适用。
主要应用就是多分类,sigmoid函数只能分两类,而softmax能分多类,softmax是sigmoid的扩展。
Logistic函数只能被使用在二分类问题中,但是它的多项式回归,即softmax函数,可以解决多分类问题。
在 softmax回归中,我们解决的是多分类问题(相对于 logistic 回归解决的二分类问题),类标  可以取
可以取  个不同的值(而不是 2 个)。因此,对于训练集
个不同的值(而不是 2 个)。因此,对于训练集  ,我们有
,我们有 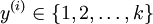 。(注意此处的类别下标从 1 开始,而不是 0)
。(注意此处的类别下标从 1 开始,而不是 0)
对于给定的测试输入  ,我们想用假设函数针对每一个类别j估算出概率值
,我们想用假设函数针对每一个类别j估算出概率值 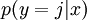 。也就是说,我们想估计
。也就是说,我们想估计  的每一种分类结果出现的概率。因此,我们的假设函数将要输出一个
的每一种分类结果出现的概率。因此,我们的假设函数将要输出一个  维的向量(向量元素的和为1)来表示这
维的向量(向量元素的和为1)来表示这  个估计的概率值。 具体地说,我们的假设函数
个估计的概率值。 具体地说,我们的假设函数 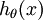 形式如下:
形式如下:
其中 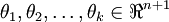 是模型的参数。请注意
是模型的参数。请注意 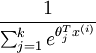 这一项对概率分布进行归一化,使得所有概率之和为 1 。
这一项对概率分布进行归一化,使得所有概率之和为 1 。
为了方便起见,我们同样使用符号  来表示全部的模型参数。在实现Softmax回归时,将
来表示全部的模型参数。在实现Softmax回归时,将  用一个
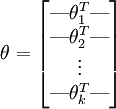
用一个 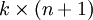 的矩阵来表示会很方便,该矩阵是将
的矩阵来表示会很方便,该矩阵是将 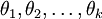 按行罗列起来得到的,如下所示:
按行罗列起来得到的,如下所示:
代价函数
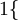 值为假的表达式
值为假的表达式 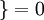 。举例来说,表达式
。举例来说,表达式 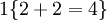 的值为1 ,
的值为1 ,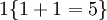 的值为 0。我们的代价函数为:
的值为 0。我们的代价函数为:
值得注意的是,上述公式是logistic回归代价函数的推广。logistic回归代价函数可以改为:
可以看到,Softmax代价函数与logistic 代价函数在形式上非常类似,只是在Softmax损失函数中对类标记的 k 个可能值进行了累加。注意在Softmax回归中将 x 分类为类别  的概率为:
的概率为:
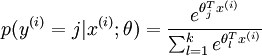 .
.
对于  的最小化问题,目前还没有闭式解法。因此,我们使用迭代的优化算法(例如梯度下降法,或 L-BFGS)。经过求导,我们得到梯度公式如下:
的最小化问题,目前还没有闭式解法。因此,我们使用迭代的优化算法(例如梯度下降法,或 L-BFGS)。经过求导,我们得到梯度公式如下:
让我们来回顾一下符号 "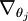 " 的含义。
" 的含义。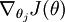 本身是一个向量,它的第
本身是一个向量,它的第  个元素
个元素 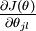 是
是  对
对 的第
的第  个分量的偏导数。
个分量的偏导数。
有了上面的偏导数公式以后,我们就可以将它代入到梯度下降法等算法中,来最小化  。 例如,在梯度下降法的标准实现中,每一次迭代需要进行如下更新:
。 例如,在梯度下降法的标准实现中,每一次迭代需要进行如下更新: 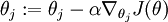 (
(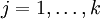 )。
)。
当实现 softmax 回归算法时, 我们通常会使用上述代价函数的一个改进版本。
Softmax回归与Logistic 回归的关系
当类别数 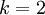 时,softmax 回归退化为 logistic 回归。这表明 softmax 回归是 logistic 回归的一般形式。具体地说,当
时,softmax 回归退化为 logistic 回归。这表明 softmax 回归是 logistic 回归的一般形式。具体地说,当 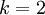 时,softmax 回归的假设函数为:
时,softmax 回归的假设函数为:
利用softmax回归参数冗余的特点,我们令 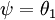 ,并且从两个参数向量中都减去向量
,并且从两个参数向量中都减去向量  ,得到:
,得到:
因此,用 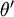 来表示
来表示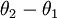 ,我们就会发现 softmax 回归器预测其中一个类别的概率为
,我们就会发现 softmax 回归器预测其中一个类别的概率为 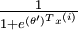 ,另一个类别概率的为
,另一个类别概率的为 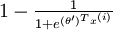 ,这与 logistic回归是一致的。
,这与 logistic回归是一致的。
广义线性模型
这些分布之所以长成这个样子,是因为我们对y进行了假设。
当y是两点分布-------->linear model
当y是正态分布-------->Logistic model
当y是多项式分布-------->Softmax
【机器学习】Softmax 和Logistic Regression回归Sigmod的更多相关文章
- Andrew Ng机器学习编程作业:Logistic Regression
编程作业文件: machine-learning-ex2 1. Logistic Regression (逻辑回归) 有之前学生的数据,建立逻辑回归模型预测,根据两次考试结果预测一个学生是否有资格被大 ...
- 【笔记】机器学习 - 李宏毅 - 6 - Logistic Regression
Logistic Regression 逻辑回归 逻辑回归与线性回归有很多相似的地方.后面会做对比,先将逻辑回归函数可视化一下. 与其所对应的损失函数如下,并将求max转换为min,并转换为求指数形式 ...
- 机器学习实战python3 Logistic Regression
代码及数据:https://github.com/zle1992/MachineLearningInAction logistic regression 优点:计算代价不高,易于理解实现,线性模型的一 ...
- Andrew Ng机器学习 二: Logistic Regression
一:逻辑回归(Logistic Regression) 背景:假设你是一所大学招生办的领导,你依据学生的成绩,给与他入学的资格.现在有这样一组以前的数据集ex2data1.txt,第一列表示第一次测验 ...
- Stanford机器学习笔记-2.Logistic Regression
Content: 2 Logistic Regression. 2.1 Classification. 2.2 Hypothesis representation. 2.2.1 Interpretin ...
- 机器学习方法(五):逻辑回归Logistic Regression,Softmax Regression
欢迎转载,转载请注明:本文出自Bin的专栏blog.csdn.net/xbinworld. 技术交流QQ群:433250724,欢迎对算法.技术.应用感兴趣的同学加入. 前面介绍过线性回归的基本知识, ...
- [机器学习] Coursera ML笔记 - 逻辑回归(Logistic Regression)
引言 机器学习栏目记录我在学习Machine Learning过程的一些心得笔记,涵盖线性回归.逻辑回归.Softmax回归.神经网络和SVM等等.主要学习资料来自Standford Andrew N ...
- 机器学习---逻辑回归(二)(Machine Learning Logistic Regression II)
在<机器学习---逻辑回归(一)(Machine Learning Logistic Regression I)>一文中,我们讨论了如何用逻辑回归解决二分类问题以及逻辑回归算法的本质.现在 ...
- 机器学习二 逻辑回归作业、逻辑回归(Logistic Regression)
机器学习二 逻辑回归作业 作业在这,http://speech.ee.ntu.edu.tw/~tlkagk/courses/ML_2016/Lecture/hw2.pdf 是区分spam的. 57 ...
随机推荐
- Quick Touch – 在 iOS 设备运行的 “Touch Bar”
关于 Quick Touch & Touch Bar Touch Bar 其实就是在原来 MBP 的按键区顶部新增了一个长条形的OLED触控屏,提供一些常用的快捷键.(iMessage 选表情 ...
- ipsec在企业网中的应用(IKE野蛮模式)(转)
from:http://lulu1101.blog.51cto.com/4455468/817954 ipsec在企业网中的应用(IKE野蛮模式) 案例: 本实验采用华为三台F100防火墙,和一台s3 ...
- YAML中重复的KEY的判断
package com.test.util; import java.io.BufferedReader; import java.io.FileInputStream; import java.io ...
- mac系统下安装mysql 和phpmyadmin
用惯了在Windows上一个appserv或phpStudy压缩包搞定,要在MAC OSX 10.10上捣腾一个PHP开发环境还不大习惯.但自己亲自配一下环境还是有所收获的.众所周知OSX上自带了ap ...
- 【Spring】SpringMVC之上传文件
这里笔者介绍利用SpringMVC上传图片的操作. 步骤 1. 引入jar文件 不仅需要导入开发SpringMVC相关的包,还需要导入 commons-fileupload-1.2.1.jar 和 ...
- 【HTML】前端性能优化之CDN和WPO的比较
CDN通过将资源存储在更接近用户的位置,缩短到服务器的往返行程,加快页面加载时间来解决性能问题.WPO解决方案,如Radware的FastView,则在前端进行性能提升处理,使页面更有效地呈现在浏览器 ...
- Mac Vim 编辑器
1.常用命令 /xxx 查找xxx n 执行上一次查找 0 到行首 w 光标往后移动一个词 b 光标往前移动一个词 x 删除当前一个字符 dw 删除一个单词 D 删除到行尾 dd 删除整行 V 选中整 ...
- [转]@PathVariable和@RequestParam的区别
请求路径上有个id的变量值,可以通过@PathVariable来获取 @RequestMapping(value = "/page/{id}", method = Request ...
- [转]用GSON 五招之内搞定任何JSON数组
关于GSON的入门级使用,这里就不提了,如有需要可以看这篇博文 <Google Gson的使用方法,实现Json结构的相互转换> ,写的很好,通俗易懂. 我为什么写这篇文章呢?因为前几晚跟 ...
- 关于thymeleaf+layout布局的使用方式,spring boot 访问页面(静态页面及jsp页面)
首先建立相同部分的html,这里我命名为layout.html,放在了`templates/layout'文件夹下,这个路径以后是会用到的,以下是我的layout的代码,比较粗糙. 但是应该会更好的帮 ...