C++动态规划实现查找最长公共子序列

问题描述：

给定两个序列X={x₁，x₂，…，x_m}和Y={y₁，y₂，…，y_n}，找出X和Y的最长公共子序列。（给定两个序列X和Y，当另一序列Z既是X的子序列又是Y的子序列时，称Z是序列X和Y的公共子序列。）

细节须知（与之前随笔的对比）：

将由数组存储起来一并输出至文件修改为边运行边输出，增加了程序的鲁棒性。

算法原理：

a.最长公共子序列的结构

对X的所有子序列，检查它是否也是Y的子序列，从而确定它是否为X和Y的公共子序列。并且在检查过程中记录最长的公共子序列。X的所有子序列都检查过后即可求出X和Y的最长公共子序列。X的每个子序列相应于下标集{1,2，…，m}的一个子集。

b.子问题的递归结构

要找出X和Y的最长公共子序列，可按以下方式递归计算：当x_m=y_n时，找出X_m-1和Y_n-1的最长公共子序列，然后在其尾部加上x_m（=y_n）即可得到X和Y的最长公共子序列。当x_m≠y_n时，必须解两个子问题，即找出X_m-1和Y的一个最长公共子序列及X和Y_n-1的一个最长公共子序列。这两个公共子序列中较长者即为X和Y的最长公共子序列。

c.计算最优值

利用动态规划算法自底向上地计算最优值。

d.构造最长公共子序列

首先从b[m][n]开始，依其值在数组b中搜索。当b[i][j]=1时，表示X_i和Y_j的最长公共子序列

 #include<cstdio>
 #include<cstring>
 #include<stack>
 #include<ctime>
 #include<iostream>
 #include<fstream>
 #include<algorithm>
 #include<windows.h>
 using namespace std;
 LARGE_INTEGER nFreq;//LARGE_INTEGER在64位系统中是LONGLONG，在32位系统中是高低两个32位的LONG，在windows.h中通过预编译宏作定义
 LARGE_INTEGER nBeginTime;//记录开始时的计数器的值
 LARGE_INTEGER nEndTime;//记录停止时的计数器的值
 #define N 10000
 //const int SIZE_CHAR = 10000; //生成32 + 1位C Style字符串
 const char CCH[] = "_0123456789abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ_";
 int dp[N][N];
 char c;
 int main(void)
 {
     //char a[N];
     //char b[N];
     //char a[SIZE_CHAR+2];
     //char b[SIZE_CHAR+2];
     ofstream fout;
     int m = ,i = ;
     int SIZE_CHAR;
     cout<<"Please enter the number of times you want to run the program:";        //输入程序运行次数
     cin>>m;
     //int SIZE[m];
     double cost;
     //double runtime[m];
     srand((unsigned)time(NULL));
     fout.open("data.txt",ios::app);
     if(!fout){
         cerr<<"Can not open file 'data.txt' "<<endl;
         return -;
     }
     fout.setf(ios_base::fixed,ios_base::floatfield);   //防止输出的数字使用科学计数法
     for(i = ; i < m; i++){
         //SIZE_CHAR=10000+RAND_MAX*(rand()%300)+rand();           //RAND_MAX=32767,随机生成数据量
         SIZE_CHAR = rand() % ;
         fout<<SIZE_CHAR<<",";
         // SIZE[i]=SIZE_CHAR;                                      //限定数据规模为10000~9872867
         char a[SIZE_CHAR + ] = {'\0'};
         char b[SIZE_CHAR + ] = {'\0'};
         cout<<"☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆The "<<i+<<"th test's string size is:"<<SIZE_CHAR<<"☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆"<<endl;
         for (int i = ; i < SIZE_CHAR; ++i){
             int x = rand() / (RAND_MAX / (sizeof(CCH) - ));
             a[i] = CCH[x];
         }
         cout<<"The first random sting is:" <<a <<endl;
         for (int i = ; i < SIZE_CHAR; ++i){
             int x = rand() / (RAND_MAX / (sizeof(CCH) - ));
             b[i] = CCH[x];
         }
         cout<<"The second random string is:" <<b <<endl;
         cout<<"The longest common subsequence is:";
         QueryPerformanceFrequency(&nFreq);//获取系统时钟频率
         QueryPerformanceCounter(&nBeginTime);//获取开始时刻计数值
         int la=strlen(a);
         int lb=strlen(b);
         memset(dp,,sizeof(dp));
         for(int i=; i<=la; i++){
             for(int j=; j<=lb; j++){
                 if(a[i-]==b[j-])
                     dp[i][j]=dp[i-][j-]+;
                 else
                     dp[i][j]=max(dp[i-][j],dp[i][j-]);
             }
         }
         int i=la,j=lb;
         stack<char>s;
         while(dp[i][j]){
             if(dp[i][j]==dp[i-][j]){//来自于左方向
                 i--;
             }
             else if(dp[i][j]==dp[i][j-]){//来自于上方向
                 j--;
             }
             else if(dp[i][j]>dp[i-][j-]){//来自于左上方向
                 i--;
                 j--;
                 s.push(a[i]);         //压栈以便倒序输出
         }
     }
     while(!s.empty())
     {
         c=s.top();
         printf("%c",c);
         s.pop();
     }
     cout<<endl;
     QueryPerformanceCounter(&nEndTime);//获取停止时刻计数值
     cost=(double)(nEndTime.QuadPart - nBeginTime.QuadPart) / (double)nFreq.QuadPart;
     fout<<cost<<endl;
     //runtime[i]=cost;
     cout<<"The running time is："<<cost<<" s"<<endl;
     }
     fout.close();
     cout<<"Success!"<<endl;
     return ;
 }

程序设计思路：

设序列X={x₁，x₂，…，x_m}和Y={y₁，y₂，…，y_n}的最长公共子序列为Z={z₁，z₂，…，z_k}，则

a.若x_m=y_n，则z_k=x_m=y_n，且Z_k-1是X_m-1和Y_n-1的最长公共子序列。

b.若x_m≠y_n，且z_k≠x_m，则Z是X_m-1和Y的最长公共子序列。

c.若x_m≠y_n，且z_k≠y_n，则Z是X和Y_n-1的最长公共子序列。

其中，X_m-1={x₁，x₂，…，x_m-1}；Y_m-1={y₁，y₂，…，y_n-1}；Z_k-1={z₁，z₂，…，z_k-1}。

② 子问题的递归结构

首先建立子问题最优值的递归关系。用c[i][j]记录序列X_i和Y_j的最长公共子序列的长度。其中，X={x₁，x₂，…，x_m}；Y={y₁，y₂，…，y_n}。当i=0或j=0时，空序列是X_i和Y_j的最长公共子序列，故此时c[i][j]=0。在其他情况下，由最优子结构性质课件里递归关系如下：

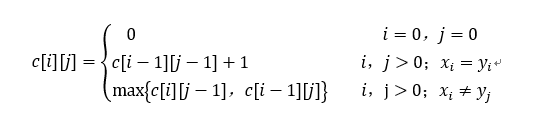
③计算最优值

以序列X和Y作为输入。输出两个数组c和b。其中c[i][j]存储X_i和Y_j的最长公共子序列的长度，b[i][j]记录c[i][j]的值是由哪一个子问题的解得到的，这在构造最长公共子序列时要用到。问题的最优值，即X和Y的最长公共子序列的长度记录与c[m][n]中。

④构造最长公共子序列

首先从b[m][n]开始，依其值在数组b中搜索。当b[i][j]=1时，表示X_i和Y_j的最长公共子序列是由X_i-1和Y_j-1的最长公共子序列在尾部加上x_i所得到的子序列；当b[i][j]=2时，表示X_i和Y_j的最长公共子序列与X_i-1和Y_j的最长公共子序列相同；当b[i][j]=3时，表示X_i和Y_j的最长公共子序列与X_i和Y_j-1的最长公共子序列相同。

时间复杂性分析：

a.计算最优值

由于每个数组单元的计算耗费O（1）的时间，此部分算法耗时为O（mn）。

b.构造最长公共子序列

该算法每一次递归调用使i或j减1，因此算法的计算时间为O（m+n）。

生成的数据可导入EXCEL中进行数据分析生成分析图表。