洛谷 P1522 牛的旅行 Cow Tours 题解

P1522 牛的旅行 Cow Tours

题目描述

农民 John的农场里有很多牧区。有的路径连接一些特定的牧区。一片所有连通的牧区称为一个牧场。但是就目前而言，你能看到至少有两个牧区通过任何路径都不连通。这样，Farmer John就有多个牧场了。

John想在牧场里添加一条路径(注意，恰好一条)。对这条路径有以下限制：

一个牧场的直径就是牧场中最远的两个牧区的距离(本题中所提到的所有距离指的都是最短的距离)。考虑如下的有5个牧区的牧场，牧区用“*”表示，路径用直线表示。每一个牧区都有自己的坐标：

                (15,15) (20,15)
                 D       E
                 *-------*
                 |     _/|
                 |   _/  |
                 | _/    |
                 |/      |
        *--------*-------*
        A        B       C
     (10,10)  (15,10) (20,10)

【请将以上图符复制到记事本中以求更好的观看效果，下同】

这个牧场的直径大约是12.07106, 最远的两个牧区是A和E，它们之间的最短路径是A-B-E。

这里是另一个牧场：

                         *F(30,15)
                        /
                      _/
                    _/
                   /
                  *------*
                  G      H
                  (25,10)   (30,10)

在目前的情景中，他刚好有两个牧场。John将会在两个牧场中各选一个牧区，然后用一条路径连起来，使得连通后这个新的更大的牧场有最小的直径。

注意，如果两条路径中途相交，我们不认为它们是连通的。只有两条路径在同一个牧区相交，我们才认为它们是连通的。

输入文件包括牧区、它们各自的坐标，还有一个如下的对称邻接矩阵

：
　 A  B  C  D  E  F  G  H
A  0  1  0  0  0  0  0  0
B  1  0  1  1  1  0  0  0
C  0  1  0  0  1  0  0  0
D  0  1  0  0  1  0  0  0
E  0  1  1  1  0  0  0  0
F  0  0  0  0  0  0  1  0
G  0  0  0  0  0  1  0  1
H  0  0  0  0  0  0  1  0

其他邻接表中可能直接使用行列而不使用字母来表示每一个牧区。输入数据中不包括牧区的名字。

输入文件至少包括两个不连通的牧区。

请编程找出一条连接两个不同牧场的路径，使得连上这条路径后，这个更大的新牧场有最小的直径。输出在所有牧场中最小的可能的直径。

输入格式

第1行: 一个整数N (1 <= N <= 150), 表示牧区数

第2到N+1行: 每行两个整数X,Y (0 <= X ,Y<= 100000), 表示N个牧区的坐标。注意每个 牧区的坐标都是不一样的。

第N+2行到第2*N+1行: 每行包括N个数字(0或1) 表示如上文描述的对称邻接矩阵。

输出格式

只有一行，包括一个实数，表示所求直径。数字保留六位小数。

只需要打到小数点后六位即可，不要做任何特别的四舍五入处理。

输入输出样例

输入 #1复制

8

10 10

15 10

20 10

15 15

20 15

30 15

25 10

30 10

01000000

10111000

01001000

01001000

01110000

00000010

00000101

00000010

输出 #1复制

22.071068

说明/提示

翻译来自NOCOW

USACO 2.4

【思路】

弗洛伊德 + 邻接矩阵

很有意思的的一道图论题

【题目分析】

两个牧场

每个牧场都有若干牧区

牧区有自己的坐标

请将任意两个所在牧区不同的牧场连接起来

使两个牧区合并为一个

同时使牧区的直径最短

（一个牧场的直径就是牧场中最远的两个牧区的距离）

【前缀思想】

这是一道图论题，嗯，没有问题

图论就要存图

这道题应该用什么来存图呢？

数据范围N<=150

很显然邻接矩阵就轻轻松松可以存起来

算法呢？

既然都用了邻接矩阵了

那弗洛伊德就来起来吧

【核心思想】

两个牧区连接起来之后

A牧区是a点和B牧区的b点连接起来

那么A牧区中其他的点到a的最大距离

加上

B牧区中其他的点到b的最大距离

是不是有很大的可能是最长直径？

这必然是可能性很大

那会影响这条新构成的链是不是最长直径的情况是什么？

是在某一个牧区中没法和另一个牧区的点相连

但是确实长度大于上面的情况

这样比较处理出每个点在图中和他相连的最长路

和两个图分开的情况下的最长路

比较输出就好了

【举例】

上面两种情况

两个点对应的最长点连接起来就是最终结果很显然

就不多赘述了

只举在两个牧场分开的情况下有边大于连起来之后的两链之和的情况



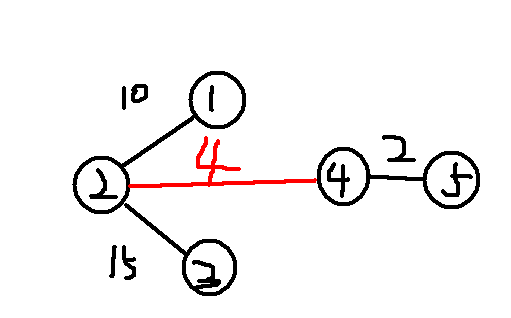
图中红色的线为自己新添加的

左边选择的点是2，右边选择的点是4

连接起来之后是15 + 4 + 2 = 21

但是在左图中

点1到点3的距离却是 25

大于21

这就是那种特殊情况

【完整代码】

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
const int Max = 155;
int x[Max],y[Max];
double f[Max][Max];
double d[Max];
int father[Max];

int main()
{
	int n;
	cin >> n;
	char c;
	for(register int i = 1;i <= n;++ i)
		father[i] = i;
	for(register int i = 1;i <= n;++ i)
		cin >> x[i] >> y[i];
	for(register int i = 1;i <= n;++ i)
	{
		for(register int j = 1;j <= n;++ j)
		{
			cin >> c;
			if(c == '1')
				f[i][j] = sqrt((x[i] - x[j]) * (x[i] - x[j]) + (y[i] - y[j]) * (y[i] - y[j]));
			else
			if(i != j)
				f[i][j] = 99999999;
		}
	}
	for(register int k = 1;k <= n;++ k)
		for(register int i = 1;i <= n;++ i)
			for(register int j = 1;j <= n;++ j)
				if(i != j && i != k && f[i][j] > f[i][k] + f[k][j])
					f[i][j] = f[j][i] = f[i][k] + f[k][j];
	double M = 0;
	for(register int i = 1;i <= n;++ i)
	{
		for(register int j = 1;j <= n;++ j)
			if(f[i][j] != 99999999)
				d[i] = max(d[i],f[i][j]);
		M = max(M,d[i]);
	}
	double Min = 999999999;
	for(register int i = 1;i <= n;++ i)
 		for(register int j = 1;j <= n;++ j)
 			if(f[i][j] == 99999999)
				Min = min(Min,d[i] + d[j] + sqrt((x[i] - x[j]) * (x[i] - x[j]) + (y[i] - y[j]) * (y[i] - y[j])));
	printf("%.6lf\n",max(Min,M));
	return 0;
}