Redis - 二进制位数组

简介

Redis 使用字符串对象来表示位数组，因为字符串对象使用的 SDS 数据结构是二进制安全的，所以程序可以直接使用 SDS 结构来保存位数组，并使用 SDS 结构的操作函数来处理位数组。

在 SDS 结构当中，buf 字节数组除了字符串结尾的 \0 空字符，其余的位置都存储着一个字节长的位数组，一个字节可以存储 8 位的二进制。

这里需要注意的是，在 buf 数组中存储的二进制位数组的顺序与实际书写的顺序相反，比如 01010101 存储在 buf 数组中的结构是 10101010 这样的倒序，使用逆序来保存位数组可以简化 SETBIT 的实现。

命令使用

Redis 提供了 GETBIT、SETBIT、BITCOUNT、BITOP、BITPOS、BITFIELD、BITFIELD_RO 等命令用于处理二进制位数组。

GETBIT

GETBIT <bitarray> <offset> 命令用于返回位数组 bitarray 在 offset 偏移量上的二进制位的值。其详细执行过程如下：

计算 byte = offset / 8 得到 offset 偏移量指定的二进制位保存在位数组的哪个字节；
计算 bit = (offset mod 8) + 1 得到 offset 偏移量指定的二进制位是 byte 字节的第几个二进制位；
根据 byte 值和 bit 值，在位数组 bitarray 中定位 offset 偏移量指定的二进制位，并返回这个位的值。

SETBIT

SETBIT <bitarray> <offset> <value> 可以看作是 GETBIT 的反向操作，只是需要注意设置二进制位时有可能需要扩展 buf 数组的长度。

具体的执行过程如下：

计算 len = (offset / 8) + 1 得到保存 offset 偏移量指定的二进制位需要多少字节；
检查 bitarray 位数组的长度是否满足要求，否则需要对 SDS 的进行扩展，并且将新增的二进制位全部置为 0；
计算 byte = offset / 8 得到 offset 偏移量指定的二进制位保存在位数组的哪个字节；
计算 bit = (offset mod 8) + 1 得到 offset 偏移量指定的二进制位是 byte 字节的第几个二进制位；
根据 byte 值和 bit 值，在位数组 bitarray 中定位 offset 偏移量指定的二进制位，首先将这个位现在的值保存在 oldvalue 变量中，然后将新值 value 设置为这个二进制位的值；
向客户端返回 oldvalue 的值。

由于 buf 数组使用逆序保存位数组，当 Redis 对 buf 数组进行扩展之后，写入操作都可以直接在新扩展的二进制位中完成，而不必改动位数组原来已有的二进制位。

BITCOUNT

BITCOUNT key [start] [end] 命令用于统计给定位数组中，值为 1 的二进制位的数量。

BITOP

BITOP operation destkey key [key ...] 支持对一个或多个保存二进制位的字符串 key 进行位元操作，并将结果保存到 destkey 上。operation 可以是 AND 、 OR 、 NOT 、 XOR 这四种操作中的任意一种：

AND: 逻辑与
OR: 逻辑或
NOT: 逻辑非
XOR: 逻辑异或

因为 BITOP AND、BITOP OR、BITOP XOR 三个命令可以接受多个位数组作为输入，程序需要遍历输入的每个位数组的每个字节来进行计算，所以这些命令的复杂度为 $O(n^2)$；与此相反，因为 BITOP NOT 命令只接受一个位数组输入，所以它的复杂度为 $O(n)$。

BITPOS

BITPOS key bit [start [end [BYTE | BIT]]] 返回字符串中设置为 1 或 0 的第一个位的位置。

默认情况下，整个字符串都会被检索一遍。命令的

使用 start 和 end 参数默认可以指定一个字节的范围，在 7.0.0 版本之后，提供了 BYTE 和 BIT 指定以字节为范围还是位为范围。

二进制位统计算法

BITCOUNT 命令要做的工作初看上去并不复杂，但实际上要高效地实现这个命令并不容易，需要用到一些精巧的算法。

遍历算法

实现 BITCOUNT 命令最简单直接的方法，就是遍历位数组中的每个二进制位，并在遇到值为 1 的二进制位时，将计数器的值增一。

遍历算法虽然实现起来简单，但效率非常低，因为这个算法在每次循环中只能检查一个二进制位的值是否为 1，所以检查操作执行的次数将与位数组包含的二进制位的数量成正比。

查表算法

查表算法就是创建一个表，表的键为某种排列的位数组，而表的值则是相应位数组中值为 1 的二进制位的数量。

创建了这种表之后，就可以根据输入的位数组进行查表，在无须对位数组的每个位进行检查的情况下，直接知道这个位数组包含了多少个值为 1 的二进制位。

初看起来，只要创建一个足够大的表，那么统计工作就可以轻易地完成，但这个问题实际上并没有那么简单，因为查表法的实际效果会受到内存和缓存两方面因素的限制：

查表法是典型的空间换时间策略，算法在计算方面节约的时间是通过花费额外的内存换取而来的，节约的时间越多，花费的内存就越大。
查表法的效果还会受到 CPU 缓存的限制，对于固定大小的 CPU 缓存来说，创建的表格越大，CPU 缓存所能保存的内容相比整个表格的比例就越少，查表时出现缓存不命中的情况就会越高，缓存的换入和换出操作就会越频繁，最终影响查表法的实际效率。

variable-precision SWAR 算法

BITCOUNT 命令要解决统计一个位数组中非 0 二进制位的数量的问题，在数学上被称为“计算汉明重量（Hamming Weight）”。目前已知效率最好的通用算法为 variable-precision SWAR 算法，该算法通过一系列位移和位运算操作，可以在常数时间内计算多个字节的汉明重量，并且不需要使用任何额外的内存。

以下是一个处理 32 位长度位数组的 variable-precision SWAR 算法的实现：

uint32_t swar(uint32_t i){

    i = (i & 0x55555555) + ((i>>1) & 0x55555555);  // 步骤 1

    i = (i & 0x33333333) + ((i>>2) & 0x33333333);  // 步骤 2

    i = (i & 0x0F0F0F0F) + ((i>>4) & 0x0F0F0F0F);  // 步骤 3

    i = (i - 0x01010101) >> 24;                    // 步骤 4

    return i;

}

variable-precision SWAR 算法实质上是通过分而治之的思想，将计算拆解成多个小问题去解决：

步骤 1 是将 32 位数组与 01010101010101010101010101010101 做逻辑与操作，并且右移 1 位之后继续做逻辑与操作，最终取它们的和。这一步的想法是将 32 位拆成每 2 位作为一个组合，统计出每一组中 1 的个数；
步骤 2 是将上述得到的结果与 00110011001100110011001100110011 做逻辑与操作。这一步的想法就是拆成每 4 位作为一个组合，统计出每一组中 1 的个数；
步骤 3 是将上述得到的结果与 00001111000011110000111100001111 做逻辑与操作。这一步的想法就是拆成每 8 位作为一个组合，统计出每一组中 1 的个数；
上述的结果仍然不是最终想要的结果，步骤 4 就是将上述得到的数字计算出 1 真正的数量。i - (0x01010101) 计算出汉明重量并记录在二进制的高八位，>> 24 语句则通过右移运算，将汉明重量移到最低八位，最后二进制对应的十进制就是汉明重量。

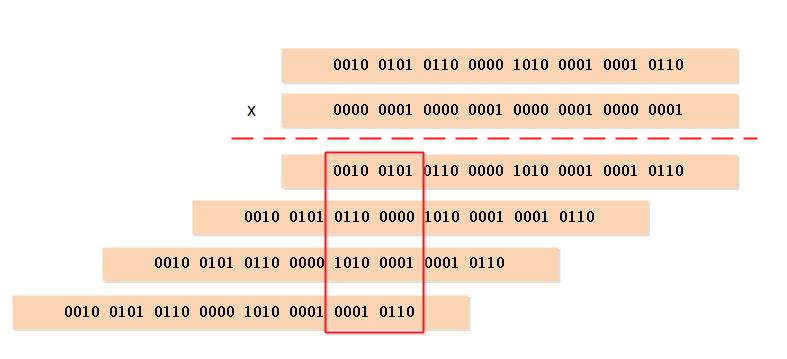
因为 variable-precision SWAR 算法是一个常数复杂度的操作，所以可以按照自己的需要，在一次循环中多次执行 variable-precision SWAR 算法，从而按倍数提升计算汉明重量的效率。

当然，在一个循环里执行多个 variable-precision SWAR 算法调用这种优化方式是有极限的：一旦循环中处理的位数组的大小超过了缓存的大小，这种优化的效果就会降低并最终消失。

Redis 的实现

BITCOUNT 命令的实现用到了查表和 variable-precision SWAR 两种算法：

如果未处理处理的二进制位的数量小于 128 位，那么程序使用查表算法来计算二进制位的汉明重量，表中记录了 0x00 ~ 0xFF 在内的所有二进制位的汉明重量
如果未处理的二进制位的数量大于等于 128 位，那么程序使用 variable-precision SWAR 算法来计算二进制位的汉明重量，每次处理 128 个二进制位，调用 4 次 32 位 variable-precision SWAR 算法来计算其汉明重量

实际上 BITCOUNT 命令实现的算法复杂度为 $O(n)$，其中 n 为输入二进制位的数量。