Weight Balanced Leafy Tree 学习笔记

前言：

在这里十分十分感谢 \(\text{lxl}\) 和王思齐发明和总结了 \(\text{WBLT}\)。
因为网上关于 \(\text{WBLT}\) 的正确讲解（已除去那篇国家集训队论文，不过伪代码和图片部分的小细节错误还是不少的）非常的少（包括 OI-Wiki 上的 \(\text{Leafy Tree}\) 和 \(\text{WBLT}\) 的专题写的也全是假的。反正基本上只要用单旋的全是假的，不服的可以把代码给我，我教你卡），所以写下了本篇笔记来和大家一起交流。
因为本人尚菜，并没有完全掌握 \(\text{WBLT}\)（也就是说，并没有做完那几道经典的 \(\text{WBLT}\) 题目），不过后面会慢慢更新。
如若想要愉快的看完本篇笔记，建议学习线段树动态开点的思想（应该算 \(\text{trick}\) 吧）。

前置知识：

一、\(\text{Leafy Tree}\)：

其实 \(\text{Leafy Tree}\) 是一类树，它的核心思想是将原始数据放在叶节点中，而非叶子节点维护区间内的信息。

听完核心思想，我想大家一定想到了一个我们喜闻乐见的数据结构——线段树。没错，线段树本质上也属于 \(\text{Leafy Tree}\)，其特征非常明显，叶子结点维护的是原始信息，而非叶子节点你想要维护的区间信息。

其实，我认为基于 \(\text{Leafy Tree}\) 的 \(\text{BST}\) 实现，其实就是一种维护区间最大值的线段树，它赋予了线段树 \(\text{BST}\) 的性质，加以去除部分的无用节点，形成一棵十分自由的线段树。

如果各位对线段树十分熟悉（尤其是动态开点），下面内容将会给你一种十分熟悉的感觉。

下面将说基于 \(\text{Leafy Tree}\) 的 \(\text{BST}\) 实现。

二、基于 \(\text{Leafy Tree}\) 的 \(\text{BST}\) 实现：

首先，我们先梳理一下 \(\text{BST}\) 和 \(\text{Leafy Tree}\) 的性质：

\(\text{BST}\)：

对于任意一棵 \(\text{BST}\) 来说，其根节点的左儿子一定不大于根节点，根节的右儿子一定不小于根节点。
插入一个节点时，其若小于等于根节点，则向左走，其若大于根节点，则向右走。

\(\text{Leafy Tree}\)：

对于任意一棵 \(\text{Leafy Tree}\) 来说，其叶子结点一定是维护的原始数据，其非叶子节点一定是维护的区间信息。
无论何时，\(\text{Leafy Tree}\) 的一个节点要么有两个儿子，要么没有儿子。

此时，根据 \(\text{Leafy Tree}\) 的性质 \(1\)，我们将所有的原始数据节点都放在叶子节点上，然后每两个节点上方加一个他们的父亲，维护的是这两个节点的最大值（注意，此时的两个节点不一定是两个原始数据节点）。

根据 \(\text{BST}\) 的性质 \(1\) 我们可以推出结论 \(1\)：

左儿子一定小于等于右儿子。

根据这一结论，我们规定 \(\text{Leafy Tree}\) 上的每一个左儿子要小于等于右儿子。

然后一棵基于 \(\text{Leafy Tree}\) 的 \(\text{BST}\) 雏形就出来了，我们再来梳理一下：

任何一个非叶子节点维护的都是其所代表的区间的最大值。
任何一个左儿子都小于等于右儿子。
真实的数据都处于叶子节点中。

根据上述内容，我们就可以实现查找了，思路如下：

如果当前要查找值小于等于当前节点的左儿子的值，则去左儿子中找，否则去右儿子找。
如果当前节点是叶子节点，则判断是否相等，若不相等，则说明没有查找值，否则找到查找值。

Code：

bool Find(PNODE T, int x){
    if(isLeaf(T))
        return T->value == x;
    if(x<=T->lchild->value)
        return Find(T->lchild,x);
    return Find(T->rchild,x);
}

现在，我们来思考插入：

若我们有一个待插入的新节点 \(x\)，则根据 \(\text{Leafy Tree}\) 的性质 \(1\)，我们不难得出这个新节点一定是在叶子上的。综合一下，就不难得出插入的思路：

如果当前待插入新节点 \(x\) 的值是小于等于当前节点左儿子的值，则进入当前节点左儿子，否则进入当前节点右儿子，然后更新当前节点（注意，一定要更新当前节点）。
如果当前节点是一个叶子结点，则进行如下操作：
- 建立两个新节点，一个的值等于当前节点的值，另一个的值等于新节点的值。
- 比较两个节点的大小，将值较大的节点设为当前节点的右儿子，较小的设为左儿子（依据性质 \(2\)）。
- 更新当前节点。

Code：

void Insert(PNODE T, int x){
    if(isLeaf(T)){
        T->lchild = newNode(x);
        T->rchild = newNode(x);
        if(T->lchild>T->rchild)
            swap(T->lchild,T->rchild);
        T->value = T->rchild->value;
        pushup(T);
        return ;
    }
    if(x<=T->lchild->value)
        Insert(T->lchild,x);
    else
        Insert(T->rchild,x);
    pushup(T);
}

那么至于删除操作，则更加的暴力：

若当前节点是叶子结点，则直接退出（因为此时我们的树为空）。
若当前节点的左儿子的值小于等于待删除的节点的值，则进行下列操作：
- 若左儿子是叶子节点，则若左儿子的值与待删除节点相同，进行下述操作：
  - 删除左儿子。
  - 将右儿子的值赋给当前节点。
  - 删除右儿子。
- 否则，就走进左儿子。
否则，对右儿子进行类似的操作。

Code：

void Delete(PNODE T, int x){
    if(isLeaf(T))
        return;
    if(x<=T->lchild->value){
        if(isLead(T->lchild)){
            if(T->lchild->value!=x)
                return;
            deleteNode(T->lchild);
            PNODE buf = T->rchild;
            *T = *buf;
            deleteNode(buf);
        }
        else
            Delete(T->lchild,x);
    }
    else{
        if(isLeaf(T->rchild)){
            if(T->rchild->value!=x)
                return;
            deleteNode(T->rchild);
            PNODE buf = T->lchild;
            *T = *buf;
            deleteNode(buf);
        }
        else
            Delete(T->rchild,x);
    }
    pushup(T);
}

三、\(\text{Weight Balanced Leafy Tree}\)：

首先，我们引入概念 \(\text{Weight Balanced Tree}\)（权平衡树，又名 \(\text{BB}\;[\alpha]\) 树），其主要思想就是依照正常的方法插入删除节点，然后如果左右子树比例不满足平衡系数 \(\alpha\) 的话，则维护平衡。

听到这一点，大家肯定想到了知名的替罪羊树。确实，替罪羊树属于 \(\text{Weight Balanced Tree}\) 的一种，其维护方式暴力重构也是 \(\text{Weight Balanced Tree}\) 的一个维护平衡的方式之一。

然而 \(\text{Weight Balanced Tree}\) 只能暴力重构维护平衡吗？显然不是，除了重构，我们还可以像 \(\text{AVL}\) 树一样旋转来维护平衡，而 \(\text{Weight Balanced Leafy Tree}\) 维护平衡的方式就是旋转。

\(\text{Weight Balanced Leafy Tree}\) 的旋转分为单旋和双旋：

单旋长这样：

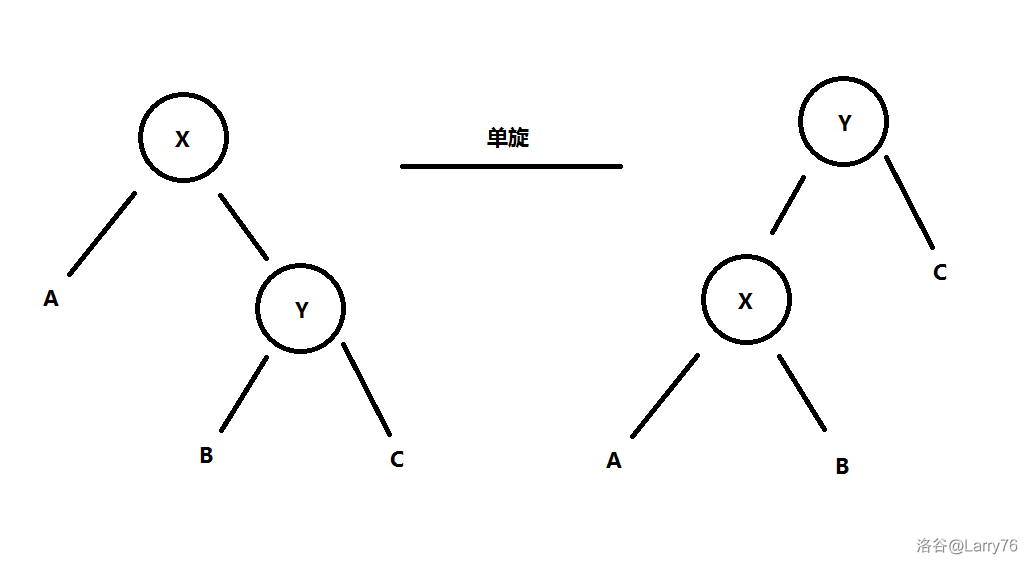
而双旋则是这样的：

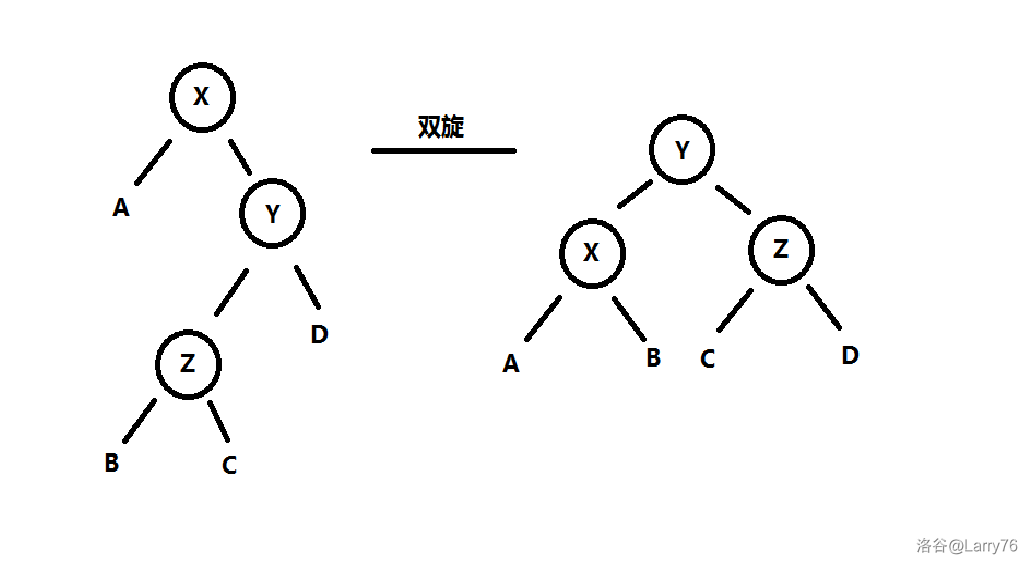
注意：再次强调，一定要有双旋，不然平衡性是假的

然后源代码和不平衡的 \(\text{Leafy Tree}\) 差不多，就是给每个节点加上属性 \(size\)，然后每次插入删除操作维护一下树的平衡并且上传的时候别忘了 \(size\) 的信息合并就可以了。

Code：

void rotate(PNODE T,bool d){
    PNODE temp;
    if(!d){
        temp = T->rchild;
        T->rchild = T->lchild;
        T->lchild = T->rchild->lchild;
        T->rchild->lchild = T->rchild->rchild;
        T->rchild->rchild = temp;
    }
    else{
        temp = T->lchild;
        T->lchild = T->rchild;
        T->rchild = T->lchild->rchild;
        T->lchild->rchild = T->lchild->lchild;
        T->lchild->lchild = temp;
    }
    pushup(T->lchild);
    pushup(T->rchild);
    pushup(T);//注意，这里一定要先 pushup 儿子，再 pushup 父亲
}

既然已经介绍完了维护平衡的方式，那么我们应当在什么时候维护平衡呢？

首先，我们设一个节点的平衡度为 \(\rho\)，\(\rho\) 的定义如下：

\[\rho_x=\dfrac{weight_{x.left}}{weight_x}
\]

其中的 \(weight_x\) 表示子树 \(x\) 所包含的叶节点数量。

那么，我们认为一个节点是平衡的当且仅当 \(\rho\) 满足 \(\rho \ge \alpha\) 且 \(1-\rho \ge \alpha\)，若当前节点不平衡，则若 \(\rho_{son} \ge \dfrac {1-2\alpha}{1-\alpha}\)，则进行双旋，否则进行单旋。

那么为什么可以依照这个原则来维护呢？我们来尝试证明一下：

我们根据单旋的图示，设 \(\rho_x\) 为节点 \(X\) 的平衡度，\(\rho_y\) 表示节点 \(Y\) 的平衡度，\(\gamma_y\) 为单旋后节点 \(\boldsymbol{Y}\) 的平衡度。

根据图示和已知条件，我们可以得出：

\[0 < \rho_x < \alpha
\]

\[\alpha \le \rho_y \le 1-\alpha
\]

根据图示和单旋的定义，我们不难看出 \(\rho_x\)、\(\rho_y\)、\(\gamma_y\) 具有以下关系：

\[\gamma_y = \rho_x + \rho_y - \rho_x\rho_y
\]

我们已知 \(\rho_x\) 和 \(\gamma_y\) 就是当前子树旋转前和旋转后的平衡度，而我们旋转后子树想要达到平衡，则需要：

\[\alpha \le \gamma_y \le 1-\alpha
\]

我们此时可以将目标拆成两部分，分别是：

\[\begin{cases}
\gamma_y \ge \alpha \\
\gamma_y \le 1 - \alpha
\end{cases}
\]

此时，将 \(\rho_x\)、\(\rho_y\)、\(\gamma_y\) 的关系代入不等式组，易得：

\[\begin{cases}
\rho_x + \rho_y - \rho_x\rho_y \ge \alpha \\
\rho_x + \rho_y - \rho_x\rho_y \le 1 - \alpha
\end{cases}
\]

将式子稍微变形，即得：

\[\begin{cases}
\rho_y \ge \dfrac {\alpha - \rho_x}{1-\rho_x} \\\\
\rho_y \le \dfrac {1 - \alpha- \rho_x}{1-\rho_x}
\end{cases}
\]

此时，我们可以得出下列两个命题：

\[1.\;\forall \rho_y \in [\alpha, 1-\alpha]\;,\; \rho_x \in [0, \alpha ]\qquad \rho_y \ge \dfrac {\alpha - \rho_x}{1-\rho_x}
\]

\[2.\;\forall \rho_y \in [\alpha, 1-\alpha]\;,\; \rho_x \in [0, \alpha ]\qquad \rho_y \le \dfrac {1- \alpha - \rho_x}{1-\rho_x}
\]

我们此时的问题也变成了证明上述两个命题在什么情况下同时成立。

命题 \(1\) 在已知条件下是显然成立的，因为原命题等于：

\[\forall \rho_y \in [\alpha, 1-\alpha]\;,\; \rho_x \in [0, \alpha ]\qquad \rho_y \ge (\dfrac {\alpha - \rho_x}{1-\rho_x})_{\max}
\]

根据糖水不等式，易得：

\[(\dfrac {\alpha - \rho_x}{1-\rho_x})_{\max} = \alpha
\]

故此时，命题 \(1\) 显然成立。

那么，关于命题 \(2\)，我们也可以有相似的证明过程：

\[\forall \rho_y \in [\alpha, 1-\alpha]\;,\; \rho_x \in [0, \alpha ]\qquad \rho_y \le (\dfrac {1 - \alpha - \rho_x}{1-\rho_x})_{\min}
\]

根据糖水不等式，易得：

\[\begin{array}{ll}
(\dfrac {1 - \alpha - \rho_x}{1 -\rho_x})_{\min} &= \dfrac{1-\alpha-\alpha}{1-\alpha}\\\\
&=\dfrac{1-2\alpha}{1-\alpha}
\end{array}
\]

代入原式，则得到：

\[\forall \rho_y \in [\alpha, 1-\alpha]\qquad \rho_y \le \dfrac{1-2\alpha}{1-\alpha}
\]

此时我们可以看出，当 \(\rho_y \in (\dfrac{1-2\alpha}{1-\alpha},1-\alpha]\) 的时候，命题二不成立，故我们需要对 \(\rho_y\) 的范围进行收缩到 \(\rho_y \in [\alpha, \dfrac{1-2\alpha}{1-\alpha}]\) 上述两个命题才同时成立。

综上，若单旋能维持平衡性，则需要 \(\rho_y \le \dfrac{1-2\alpha}{1-\alpha}\)，否则则必须进行双旋。

证毕。

所以此时的维护应当这么写：

若当前节点左儿子的大小与当前节点的大小的比值小于 \(\alpha\)，则：
- 若当前右儿子的左儿子的大小与当前右儿子的大小的比值大于等于 \(\dfrac{1-2\alpha}{1-\alpha}\)，则进行双旋。
- 否则进行单旋。
否则若当前节点右儿子的大小与当前节点的大小的比值小于 \(\alpha\)，则：
- 若当前左儿子的右儿子的大小与当前左儿子的大小的比值大于等于 \(\dfrac{1-2\alpha}{1-\alpha}\)，则进行双旋。
- 否则进行单旋。

Code：

void maintain(PNODE T){
    if(!isLeaf(T)){
        if(T->lchild->size < T->size * alpha)
            d = 1;
        else if(T->rchild->size < T->size * alpha)
            d = 0;
        else
            return;
        if(d){
            if(T->rchild->lchild->size >= T->rchild->size * (1-2*alpha)/(1-alpha))
                rotate(T->rchild,!d);
        }
        else
            if(T->lchild->rchild->size >= T->lchild->size * (1-2*alpha)/(1-alpha))
                rotate(T->lchild,!d);
        rotate(T,d);
        pushup(T);
    }
}

关于平衡因子 \(\alpha\) 的取值问题，实际上只要取在区间 \([0,\dfrac{3-\sqrt{5}}{2}]\) 之间的话都可以，证明太显然了，在这里受篇幅限制就不展开了，证明思路就考虑区间的定义即可，具体参见高一集合部分。个人实践得出 \(\alpha\) 最佳取值是 \(0.2928\)，不过具体而言则是因题而异。

附普通平衡树板子：

\(\text{Code}\)

四、\(\text{Weight Balanced Leafy Tree}\) 的区间操作：

既然 \(\text{WBLT}\) 和线段树这么像，那么我们是不是可以按照线段树的方法对其进行区间操作呢？答案是可以的，但是仅针对于线段树所能维护的操作这样打标记。

例如，我们利用 \(\text{WBLT}\) 过掉线段树板板题的时候就可以这么干，不过碍于篇幅限制，我就只好将代码扔到云剪贴板里了，有兴趣的可以去看看。

不过，如果遇到线段树维护不了的操作，我们的 \(\text{WBLT}\) 就束手无策……了吗？

其实并没有，因为 \(\text{WBLT}\) 可以分裂和合并的特性（实际上这个特性是从线段树继承过来的），加之平衡树的高度自由性，我们不难想到可以用类似 \(\text{FHQ Treap}\) 的方法来进行维护一些线段树特性所不支持的操作（因为他毕竟不能像 \(\text{Splay}\) 那样把区间旋上去）。

不过，\(\text{WBLT}\) 的 \(\operatorname{Split}\) 和 \(\operatorname{Merge}\) 操作并不像 \(\text{FHQ Treap}\) 那么好写（并且常数还大了），因为 \(\operatorname{Merge}\) 和 \(\operatorname{Split}\) 操作有可能会让原先的 \(\text{WBLT}\) 失去其自身的性质，这可能也是 \(\text{WBLT}\) 为数不多的痛点吧（不过也有可能自己写丑了）。

现在，我们考虑合并操作，对于给定的两棵树 \(A\) 和 \(B\)：

若 \(size_B \ge size_A \cdot \alpha\) 则直接将 \(A\)、\(B\) 合并，即将 \(A\) 设为右儿子，\(B\) 设为左儿子。
否则，进行下述操作：
- 若 \(size_A \ge size_B\)：
  - 若将 \(B\) 直接合并到 \(A\) 的右儿子能保持平衡，那就合并，然后其结果再与 \(A\) 的左儿子合并。
  - 否则，将 \(A\) 的左儿子的右儿子与 \(A\) 的右儿子进行合并，将 \(A\) 的左儿子的左儿子与 \(B\) 进行合并，再将两者的合并结果进行合并。
- 否则：
  - 若将 \(A\) 直接合并到 \(B\) 的左儿子能保持平衡，那就合并，然后其结果再与 \(B\) 的右儿子合并。
  - 否则，将 \(A\) 与 \(B\) 的左儿子的左儿子合并，将 \(B\) 的左儿子的右儿子与 \(B\) 的右儿子进行合并，再将两者的结果进行合并。

实际上，\(\operatorname{Merge}\) 的函数其实本质上就是：若两者直接合并平衡，则直接合并，否则单旋后合并，否则双旋后合并。

Code：

inline PNODE Merge(PNODE a,PNODE b) //打大写太麻烦了，只好用小写了/kel
{
    if(a==nullptr)
        return b;
    if(b==nullptr)
        return a;
    if(b->size >= a->size * alpha / (1-alpha))//能直接合并则直接合并
        return mix(a,b);
    PNODE ret = nullptr;
    if(a->size > b->size){
        pushdown(a);
        if(a->lchild->size >= (a->size + b->size) * alpha){
            ret = Merge(a->lchild, Merge(a->rchild,b));
            deleteNode(a);//此时原节点 a 变成了垃圾节点，要回收空间
            return ret;
        }
        pushdown(a->rchild);
        ret = Merge(Merge(a->lchild, a->rchild->lchild), Merge(a->rchild->rchild, b));
        deleteNode(a);//此时原节点 a 变成了垃圾节点，要回收空间
        return ret;
    }
    else{
        pushdown(b);
        if(b->rchild->size >= (a->size + b->size) * alpha){
            ret = Merge(Merge(a, b->lchild), b->rchild);
            deleteNode(b);//此时原节点 b 变成了垃圾节点，要回收空间
            return ret;
        }
        pushdown(b->lchild);
        ret = Merge(Merge(a, b->lchild->lchild), Merge(b->lchild->rchild, b->rchild));
        deleteNode(b);//此时原节点 b 变成了垃圾节点，要回收空间
        return ret;
    }
}

注意：\(\boldsymbol{\operatorname{Merge}}\) 操作不满足交换律。

有了 \(\operatorname{Merge}\) 了以后，\(\operatorname{Split}\) 就好写多了（实际上也没好写到哪里去）。

\(\text{WBLT}\) 的 \(\operatorname{Split}\) 实际上也可以分为两种，分别是“按秩分裂”和“按值分裂”。

我们先谈谈按秩分裂。

我们思考一下，若当前还要分裂的大小为 \(0\) 了，那么我们还需要分裂吗？显然不需要了。故此时我们就可以将分裂出来的树 \(X\) 置为空。

那么如果当前要分裂的树是一个叶子节点，那么我们显然也不需要分类了，直接将树 \(X\) 置为当前树 \(T\) 就行了。

否则的话，我们首先将标记下传，然后如果当前待分裂的大小小于等于我们左子树的大小，则先将左子树分裂成两部分，一部分是我们需要的，另一部分是分剩下的。

此时 Merge 就派上用场了，将剩下的和树 \(T\) 的左子树进行合并，就是我们需要的另一部分树 \(Y\)。

对于右子树，我们进行类似的操作，只不过在分裂右子树时所用的大小应当是原大小减去左子树大小。

Code:

// 先行注意，传参之前请先将子树 X 和 Y 置为 nullptr。
void Split(PNODE T, int x, PNODE &X, PNODE &Y){
    if(!x){
        Y = T;
        return;
    }
    if(isLeaf(T)){
        X = T;
        return ;
    }
    pushdown(T);
    if(x<=X->lchild->size){
        PNODE bufY = nullptr;
        Split(T->lchild, x, X, bufY);
        Y = Merge(bufY,T->rchild);
    } else {
        PNODE bufX = nullptr;
        Split(T->rchild, x - T->lchild->size, bufX, Y);
        X = Merge(T->lchild, bufX);
    }
}

至于按值分裂，实际上和按秩分裂是一模一样的，只不过按值分裂不需要判断 \(x\) 是否为 \(0\)，且分裂右子树的时候不需要将 \(x\) 减去左子树的大小，剩下就基本上一模一样了。碍于篇幅限制，我们就不进行进一步的代码演示了。

注意：若 \(\operatorname{Merge}\) 和 \(\operatorname{Split}\) 执行次数过多，则会产生无法接受的垃圾节点数量，故我们在写 \(\operatorname{Merge}\) 和 \(\operatorname{Split}\) 的时候，请务必做好垃圾回收！！

附文艺平衡树代码：

\(\text{Code}\)

五、\(\text{Weight Balanced Leafy Tree}\) 实现可并堆：

在讲 \(\text{WBLT}\) 的可持久化之前，我们先讲点整活的部分。

目前好像是没有找到哪一篇文章写 \(\text{WBLT}\) 怎么实现可并堆，不过可能是因为其思路过于简单或者是左偏树实在是太好写了。

按照惯例，我们先来回顾一下堆的性质：

根节点大于等于或小于等于其所有的儿子节点
堆是一棵完全二叉树。

然后，我们把目光放到所有 \(\text{WBLT}\) 节点上，尤其是非叶子节点上，就可以看到一些平时在平衡树上所看不到的东西：

父节点维护的是其表示的区间的最大值。

诶，等等，这不就意味着父节点是它所代表的区间内的值最大的节点吗？确实，所以我们此时不难看出，\(\text{WBLT}\) 的本身也是满足堆的性质 \(1\) 的。

至于性质 \(2\)，兄弟，这是平衡树啊！！所以 \(\text{WBLT}\) 是可以当堆使的。

又因为 \(\text{WBLT}\) 支持合并，所以自然而然的就可以做可并堆来使了。

碍于篇幅限制，我将过掉可并堆模板题的代码放到云剪贴板里面了，有兴趣的大家可以去康一康，顺便看看有没有什么数据能把它卡掉，这里就不多赘述了。