神经网络入门篇：详解搭建神经网络块（Building blocks of deep neural networks）

搭建神经网络块

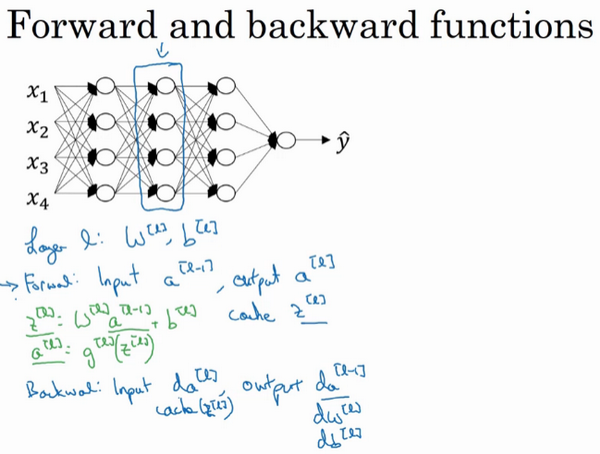
这是一个层数较少的神经网络，选择其中一层（方框部分），从这一层的计算着手。在第\(l\)层有参数\(W^{[l]}\)和\(b^{[l]}\)，正向传播里有输入的激活函数，输入是前一层\(a^{[l-1]}\)，输出是\(a^{[l]}\)，之前讲过\(z^{[l]} =W^{[l]}a^{[l-1]} +b^{[l]}\),\(a^{[l]} =g^{[l]}(z^{[l]})\)，那么这就是如何从输入\(a^{[l-1]}\)走到输出的\(a^{[l]}\)。之后就可以把\(z^{[l]}\)的值缓存起来，在这里也会把这包括在缓存中，因为缓存的\(z^{[i]}\)对以后的正向反向传播的步骤非常有用。

然后是反向步骤或者说反向传播步骤，同样也是第\(l\)层的计算，会需要实现一个函数输入为\(da^{[l]}\)，输出\(da^{[l-1]}\)的函数。一个小细节需要注意，输入在这里其实是\(da^{[l]}\)以及所缓存的\(z^{[l]}\)值，之前计算好的\(z^{[l]}\)值，除了输出\(da^{[l-1]}\)的值以外，也需要输出需要的梯度\(dW^{[l]}\)和\(db^{[l]}\)，这是为了实现梯度下降学习。

这就是基本的正向步骤的结构，把它成为称为正向函数，类似的在反向步骤中会称为反向函数。总结起来就是，在l层，会有正向函数，输入\(a^{[l-1]}\)并且输出\(a^{[l]}\)，为了计算结果需要用\(W^{[l]}\)和\(b^{[l]}\)，以及输出到缓存的\(z^{[l]}\)。然后用作反向传播的反向函数，是另一个函数，输入\(da^{[l]}\)，输出\(da^{[l-1]}\)，就会得到对激活函数的导数，也就是希望的导数值\(da^{[l]}\)。\(a^{[l-1]}\)是会变的，前一层算出的激活函数导数。在这个方块（第二个）里需要\(W^{[l]}\)和\(b^{[l]}\)，最后要算的是\(dz^{[l]}\)。然后这个方块（第三个）中，这个反向函数可以计算输出\(dW^{[l]}\)和\(db^{[l]}\)。

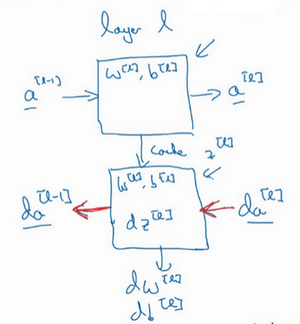
然后如果实现了这两个函数（正向和反向），然后神经网络的计算过程会是这样的：

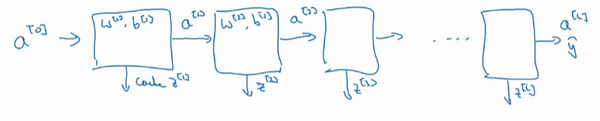
把输入特征\(a^{[0]}\)，放入第一层并计算第一层的激活函数，用\(a^{[1]}\)表示，需要\(W^{[1]}\)和\(b^{[1]}\)来计算，之后也缓存\(z^{[l]}\)值。之后喂到第二层，第二层里，需要用到\(W^{[2]}\)和\(b^{[2]}\)，会需要计算第二层的激活函数\(a^{[2]}\)。后面几层以此类推，直到最后算出了\(a^{[L]}\)，第\(L\)层的最终输出值\(\hat y\)。在这些过程里缓存了所有的\(z\)值，这就是正向传播的步骤。

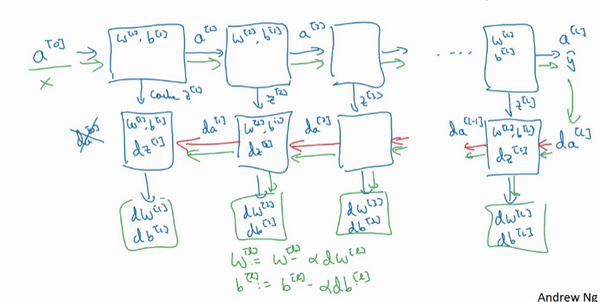
对反向传播的步骤而言，需要算一系列的反向迭代，就是这样反向计算梯度，需要把\(da^{[L]}\)的值放在这里，然后这个方块会给\({da}^{[L-1]}\)的值，以此类推，直到得到\({da}^{[2]}\)和\({da}^{[1]}\)，还可以计算多一个输出值，就是\({da}^{[0]}\)，但这其实是的输入特征的导数，并不重要，起码对于训练监督学习的权重不算重要，可以止步于此。反向传播步骤中也会输出\(dW^{[l]}\)和\(db^{[l]}\)，这会输出\(dW^{[3]}\)和\(db^{[3]}\)等等。

神经网络的一步训练包含了，从\(a^{[0]}\)开始，也就是 \(x\) 然后经过一系列正向传播计算得到\(\hat y\)，之后再用输出值计算这个（第二行最后方块），再实现反向传播。现在就有所有的导数项了，\(W\)也会在每一层被更新为\(W=W-αdW\)，\(b\)也一样，\(b=b-αdb\)，反向传播就都计算完毕，有所有的导数值，那么这是神经网络一个梯度下降循环。

继续下去之前再补充一个细节，概念上会非常有帮助，那就是把反向函数计算出来的\(z\)值缓存下来。当做编程练习的时候去实现它时，会发现缓存可能很方便，可以迅速得到\(W^{[l]}\)和\(b^{[l]}\)的值，非常方便的一个方法，在编程练习中缓存了\(z\)，还有\(W\)和\(b\)对吧？从实现角度上看，认为是一个很方便的方法，可以将参数复制到在计算反向传播时所需要的地方。

现在们见过实现深度神经网络的基本元件，在每一层中有一个正向传播步骤，以及对应的反向传播步骤，以及把信息从一步传递到另一步的缓存。