【LeetCode二叉树#10】从中序与后序（或者前序）遍历序列构造二叉树（首次构造二叉树）

从中序与后序遍历序列构造二叉树

力扣题目链接(opens new window)

根据一棵树的中序遍历与后序遍历构造二叉树。

注意: 你可以假设树中没有重复的元素。

例如，给出

中序遍历 inorder = [9,3,15,20,7] 后序遍历 postorder = [9,15,7,20,3] 返回如下的二叉树：

思路

题目给了目标二叉树的中序遍历（左中右）和后序遍历（左右中）结果数组

那么我们可以通过后序遍历的结果数组的最后一个值确定该二叉树的根节点

有了根节点，下一步就要确定根节点两侧的树的节点，这时就需要使用根节点分别在中序和后序结果数组中分割(一定是先中序再后序)

按顺序在中序遍历和后序遍历的结果数组中使用该值进行数组分割(注意，这里的左右是针对当前所分割的数组来说的)

• 先分割中序遍历的结果数组，得到中序左数组和中序右数组
• 再分割后序遍历的结果数组，得到后序左数组和后序右数组

完成分割之后，再使用递归对左右区间进行相同的处理，直到最后碰到叶子节点

图示如下：

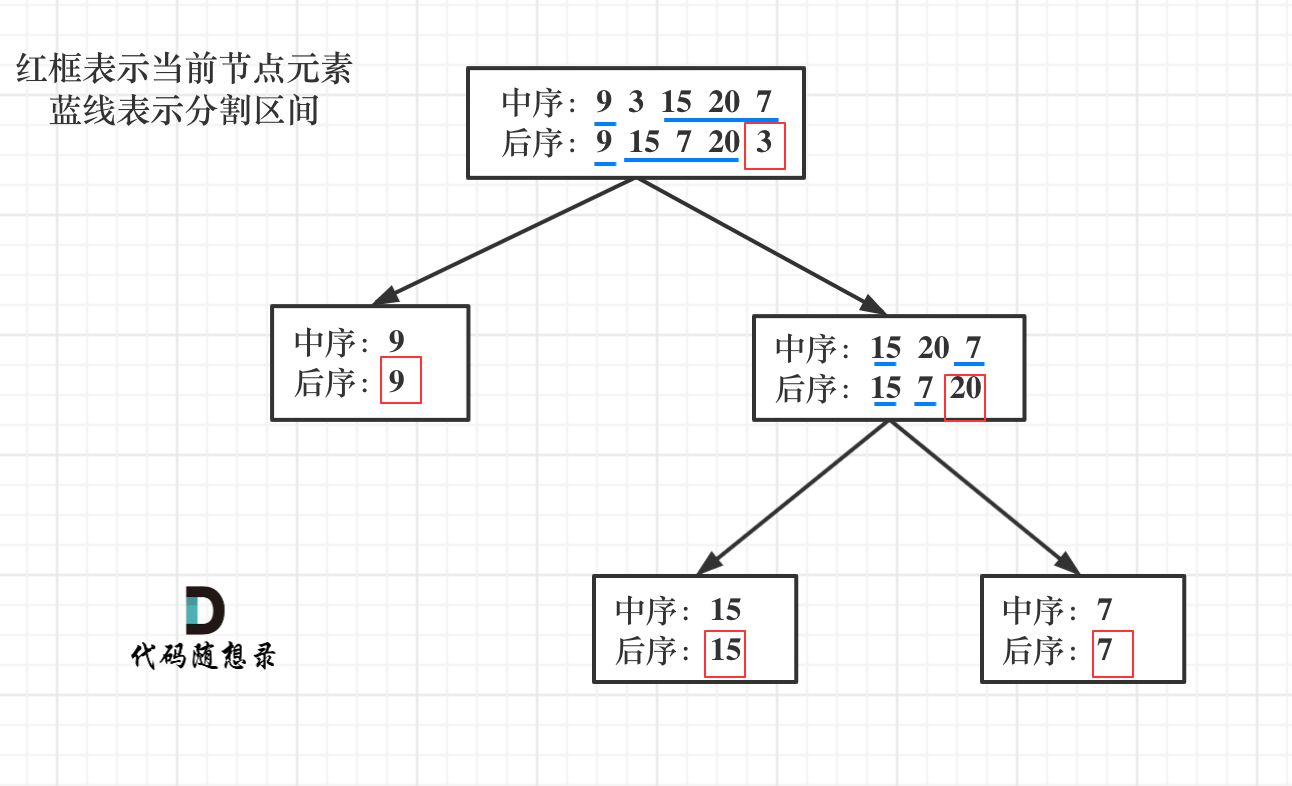
上图例子中，先通过后序遍历数组（[9,15,7,20,3]）的最后一个数确认根节点（中间节点） 3

先在中序遍历数组（[9,3,15,20,7]）中按 3 进行分割，得到左边部分（[9]）和右边部分（[15,20,7]），即中序左数组和中序右数组

然后在后序遍历数组（[9,15,7,20,3]）中进行分割

因为 3 在后序遍历数组的最后一位，所以不能用来做分割点位，并且也不能继续保留了

那怎么分割后序数组呢？

这里有一个规律：中序遍历数组和后序遍历数组在整体大小上永远是相同的

我们既然已经分割好了中序遍历数组，那么就可以根据左边中序遍历数组（不能是右边）的大小来对后序遍历数组进行分割

后序遍历数组（[9,15,7,20,3]）分割好后得到左边部分（[9]）和右边部分（[15,7,20]），即后序左数组和后序右数组

此时我们需要进行递归对 左中序/后序 和 右中序/后序 进行处理，处理逻辑同上（也是使用后序数组确定中节点，分割中序数组，再通过中序数组分割后序数组）

代码

代码实现的步骤一共分以下几步：

• 第一步：如果数组大小为零的话，说明是空节点了。
• 第二步：如果不为空，那么取后序数组最后一个元素作为节点元素。
• 第三步：找到后序数组最后一个元素在中序数组的位置，作为切割点
• 第四步：切割中序数组，切成中序左数组和中序右数组 （顺序别搞反了，一定是先切中序数组）
• 第五步：切割后序数组，切成后序左数组和后序右数组
• 第六步：递归处理左区间和右区间

本题的代码比较多，可以先把整体框架写出来再补充

框架

//递归函数的返回值应
TreeNode* traversal(vector<int>& inorder, vector<int>& postorder){
    //确认数组是否为0
    if(postorder.size() == 0) return NULL;

    //后序遍历数组的最后一个数，即根节点
    int rootValue = postorder[postorder.size() - 1];
    //创建根节点
    TreeNode* root = new TreeNode(rootValue);

    //如果当前postorder只有一个值，那根节点就是叶子节点，可直接返回
    if(postorder.size() == 1) return root;

    //遍历中序遍历数组，寻找切割点
    //注意，是在中序遍历数组找出与rootValue值相同的元素的 下标
    int cutIndex;
    for(cutIndex = 0; cutIndex < inorder.size(); ++cutIndex){
        //遇到目标值就结束遍历
        if(inorder[cutIndex] == rootValue) break;
    }

    // 第四步：切割中序数组，得到 中序左数组和中序右数组
    // 第五步：切割后序数组，得到 后序左数组和后序右数组

    //第六步，调用递归处理root两侧的节点
    root->left = traversal(中序左数组, 后序左数组);
    root->right = traversal(中序数右组, 后序右数组);
}

切割数组

定义vector保存切割中序/后序数组的结果

//递归函数的返回值应
TreeNode* traversal(vector<int>& inorder, vector<int>& postorder){
    ...

    //遍历中序遍历数组，寻找切割点
    //注意，是在中序遍历数组找出与rootValue值相同的元素的 下标
    int cutIndex;
    for(cutIndex = 0; cutIndex < inorder.size(); ++cutIndex){
        //遇到目标值就结束遍历
        if(inorder[cutIndex] == rootValue) break;
    }

    // 第四步：切割中序数组，得到 中序左数组和中序右数组
    // 左闭右开区间：[0, delimiterIndex)
    vector<int> leftInorder(inorder.begin(), inorder.begin() + cutIndex);
    vector<int> rightInorder(inorder.begin() + cutIndex + 1, inorder.end());
    // 第五步：切割后序数组，得到 后序左数组和后序右数组
    // 先把后序数组里面的最后一个元素舍弃，，那个节点已经作为根节点了
    postorder.resize(postorder.size() - 1);
    vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
    vector<int> rightPostorder(postorder.begin() + leftInorder.size() + 1, postorder.end());
    ...
}

之后再调用递归，按照相同逻辑重复处理分割出来的区间

完整代码

class Solution {
public:
    //递归函数的返回值应
    TreeNode* traversal(vector<int>& inorder, vector<int>& postorder){
        //确认数组是否为0
        if(postorder.size() == 0) return NULL;

        //后序遍历数组的最后一个数，即根节点
        int rootValue = postorder[postorder.size() - 1];
        //创建根节点
        TreeNode* root = new TreeNode(rootValue);

        //如果当前postorder只有一个值，那根节点就是叶子节点，可直接返回
        if(postorder.size() == 1) return root;

        //遍历中序遍历数组，寻找切割点
        //注意，是在中序遍历数组找出与rootValue值相同的元素的 下标
        int cutIndex;
        for(cutIndex = 0; cutIndex < inorder.size(); ++cutIndex){
            //遇到目标值就结束遍历
            if(inorder[cutIndex] == rootValue) break;
        }

        // 第四步：切割中序数组，得到 中序左数组和中序右数组
        // 左闭右开区间：[0, delimiterIndex)
        vector<int> leftInorder(inorder.begin(), inorder.begin() + cutIndex);
        // [delimiterIndex + 1, end)
        // 这里加1是为了跳过根节点3
        vector<int> rightInorder(inorder.begin() + cutIndex + 1, inorder.end());
        // 第五步：切割后序数组，得到 后序左数组和后序右数组
        // 先把后序数组里面的最后一个元素舍弃，那个节点已经作为根节点了
        // 依然左闭右开，注意这里使用了左中序数组大小作为切割点
        // [0, leftInorder.size)
        postorder.resize(postorder.size() - 1);
        vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
        // [leftInorder.size(), end)
        //这里不用加1是因为3已经在前面被删除了
        vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());

        /*// 以下为日志
        cout << "----------" << endl;

        cout << "leftInorder :";
        for (int i : leftInorder) {
            cout << i << " ";
        }
        cout << endl;

        cout << "rightInorder :";
        for (int i : rightInorder) {
            cout << i << " ";
        }
        cout << endl;

        cout << "leftPostorder :";
        for (int i : leftPostorder) {
            cout << i << " ";
        }
        cout << endl;
         cout << "rightPostorder :";
        for (int i : rightPostorder) {
            cout << i << " ";
        }
        cout << endl;*/

        //第六步，调用递归处理root两侧的节点
        root->left = traversal(leftInorder, leftPostorder);
        root->right = traversal(rightInorder, rightPostorder);

        return root;
    }

    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        //判断所给数组是否为空
        if (inorder.size() == 0 || postorder.size() == 0) return NULL;
        return traversal(inorder, postorder);
    }
};

注意点

0、先把框架写了再填内容

1、分割中序数组时，记得不要把3再加进来

2、别忘了vector的构造方式

void test01()
{
	vector<int> v1; //无参构造
	for (int i = 0; i < 10; i++)
	{
		v1.push_back(i);
	}
	printVector(v1);

	vector<int> v2(v1.begin(), v1.end());
	printVector(v2);

	vector<int> v3(10, 100);
	printVector(v3);

	vector<int> v4(v3);
	printVector(v4);
}

从前序与中序遍历序列构造二叉树

力扣题目链接(opens new window)

根据一棵树的前序遍历与中序遍历构造二叉树。

注意: 你可以假设树中没有重复的元素。

例如，给出

前序遍历 preorder = [3,9,20,15,7] 中序遍历 inorder = [9,3,15,20,7] 返回如下的二叉树：

思路

与使用 中序+后序 构造的思路一致

只是这里最开始时，我们需要从前序遍历数组中找根节点（即第一个元素）

代码

class Solution {
public:
    TreeNode* traversal(vector<int>& preorder, vector<int>& inorder){
        //从前序数组拿根节点，先判断其是否为空
        if(preorder.size() == 0) return NULL;

        //获取根节点数值
        int rootValue = preorder[0];
        //创建根节点
        TreeNode* root = new TreeNode(rootValue);

        //如果只有一个根节点，返回
        if(preorder.size() == 1) return root;

        //在中序数组中遍历出与根节点相同值的元素的下标
        int cutIndex;
        for(cutIndex = 0; cutIndex < inorder.size(); ++cutIndex){
            if(inorder[cutIndex] == rootValue) break;
        }

        //分割中序数组
        vector<int> leftInorder(inorder.begin(), inorder.begin() + cutIndex);
        vector<int> rightInorder(inorder.begin() + cutIndex + 1, inorder.end());

        //分割前序数组
        vector<int> leftPreorder(preorder.begin() + 1, preorder.begin() + 1 + leftInorder.size());
        vector<int> rightPreorder(preorder.begin() + 1 + leftInorder.size(), preorder.end());

        // // 以下为日志
        // cout << "----------" << endl;

        // cout << "leftInorder :";
        // for (int i : leftInorder) {
        //     cout << i << " ";
        // }
        // cout << endl;

        // cout << "rightInorder :";
        // for (int i : rightInorder) {
        //     cout << i << " ";
        // }
        // cout << endl;

        // cout << "leftPreorder :";
        // for (int i : leftPreorder) {
        //     cout << i << " ";
        // }
        // cout << endl;
        //  cout << "rightPreorder :";
        // for (int i : rightPreorder) {
        //     cout << i << " ";
        // }
        // cout << endl;

        //递归处理
        root->left = traversal(leftPreorder, leftInorder);
        root->right = traversal(rightPreorder, rightInorder);

        return root;
    }

    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        return traversal(preorder, inorder);
    }
};