线性判别分析（LDA）：降维与分类的完美结合

在机器学习领域，线性判别分析（Linear Discriminant Analysis，简称LDA）是一种经典的算法，它在降维和分类任务中都表现出色。

LDA通过寻找特征空间中能够最大化类间方差和最小化类内方差的方向，实现数据的降维和分类。

本文主要介绍LDA的基本原理，展示其如何解决分类问题，以及在高维度数据降维中的应用。

1. 基本原理

简单来说，线性判别分析(LDA)旨在找到一个线性组合，将数据投影到低维空间，使得不同类别的数据尽可能地分开，同一类别的数据尽可能地紧凑。

它通过寻找一个投影方向，使得投影后不同类别之间的方差最大，而同一类别内部的方差最小。

寻找投影方向时，LDA基于费舍尔判别准则，该准则通过最大化类间散度与类内散度的比值来寻找最佳投影方向。

LDA基本的计算步骤如下：

1. 计算类内散度矩阵：衡量同一类别内数据点的分布
2. 计算类间散度矩阵：衡量不同类别之间的分布
3. 求解广义特征值问题：找到最大化类间距离与类内距离比值的投影方向
4. 选择最优投影方向：将数据投影到低维空间，同时保留分类信息

2. 如何有效降维数据

LDA在处理高维数据时具有显著优势，它通过将数据投影到低维空间，同时保持类别之间的分离度，来实现降维。

下面的示例演示如何使用LDA来实现数据的降维。

首先选择scikit-learn库中经典的鸢尾花数据集，这个数据集中每个数据有4个维度：花瓣的长度和宽度，花萼的长度和宽度。

整个数据集包含3个类别的鸢尾花。

下面通过LDA把数据集降低为2维，然后看看3个类别的鸢尾花在2维空间中是否能区分开来。

from sklearn.datasets import load_iris
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
import matplotlib.pyplot as plt

# 加载鸢尾花数据集
iris = load_iris()
X = iris.data
y = iris.target

# 创建LDA模型，指定降维后的特征数量为2
lda = LinearDiscriminantAnalysis(n_components=2)

# 训练模型并降维
X_lda = lda.fit_transform(X, y)

# 绘制降维后的数据
plt.scatter(X_lda[:, 0], X_lda[:, 1], c=y, cmap='viridis', edgecolors='k')
plt.xlabel('LD1')
plt.ylabel('LD2')
plt.title('LDA 降低到2维')
plt.show()

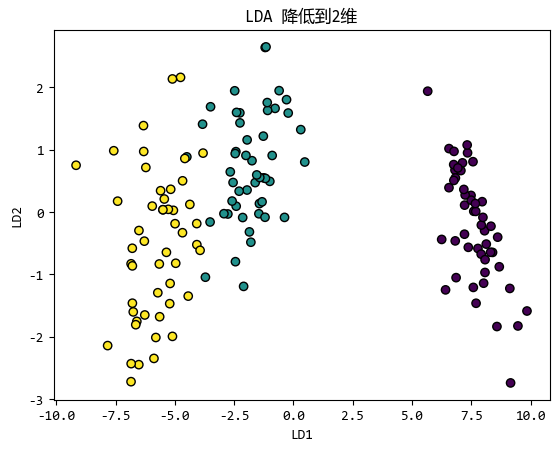
从图中我们可以看出，虽然鸢尾花数据集从四个特征降维到两个维度。

但是，通过可视化降维后的数据，可以看到不同类别的数据点在新的二维空间中仍然保持了良好的分离度。

下面再试试一个更高维度数据的降维，使用scikit-learn库中的手写数字数据集（MNIST）。

这个数据集中的每个数字图片是一个28x28的矩阵，也就是一个784维的数据。

我们将其降维到2维，看看效果如何。

from sklearn.datasets import load_digits
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
import matplotlib.pyplot as plt

# 加载手写数字数据集
digits = load_digits()
X = digits.data
y = digits.target

# 创建LDA模型，降维到2维
lda = LinearDiscriminantAnalysis(n_components=2)

# 训练并投影数据
X_lda = lda.fit_transform(X, y)

# 可视化降维后的数据
plt.figure()
ten_colors = plt.get_cmap("tab10")(range(10))
for c, i, target_name in zip(ten_colors, [0, 1, 2, 3, 4, 5, 6,7,8,9], ['0', '1', '2', '3', '4', '5', '6', '7', '8', '9']):
    plt.scatter(X_lda[y == i, 0], X_lda[y == i, 1], color=c, label=target_name)
plt.title('LDA降维后的手写数字数据')
plt.xlabel('LDA 1')
plt.ylabel('LDA 2')
plt.legend()
plt.show()

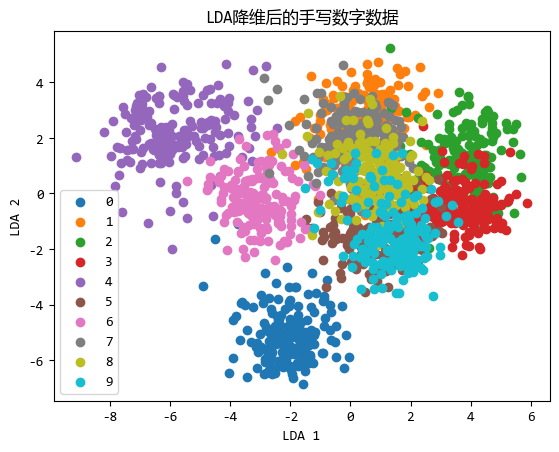
从图中可以看出，0,2,3,4,6分离的还不错，但是1,5,8,9这几个数字映射到2维时重合的比较多。

不过，从784维降低到2维，还能有这样的区分度，LDA已经算是比较厉害了。

3. 如何处理分类问题

除了进行数据降维，LDA也可以处理分类问题，同样上面的鸢尾花数据集，这次不降维直接训练模型进行分类。

import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# 加载数据集
data = load_iris()
X = data.data
y = data.target

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 创建LDA模型
lda = LinearDiscriminantAnalysis()

# 训练模型
lda.fit(X_train, y_train)

# 预测
y_pred = lda.predict(X_test)

# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print(f"分类准确率: {accuracy:.2f}")

## 输出结果：
# 分类准确率: 1.00

从结果来看，LDA分类的准确率高达100%。

再试试高维度的手写数字数据集（MNIST）。

from sklearn.datasets import load_digits
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
import matplotlib.pyplot as plt

# 加载手写数字数据集
digits = load_digits()
X = digits.data
y = digits.target

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 创建LDA模型
lda = LinearDiscriminantAnalysis()

# 训练模型
lda.fit(X_train, y_train)

# 预测
y_pred = lda.predict(X_test)

# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print(f"分类准确率: {accuracy:.2f}")

## 输出结果：
# 分类准确率: 0.95

效果还不错，也有95%的准确率。

4. 总结

线性判别分析（LDA）是一种经典的线性模型，它在降维和分类任务中都表现出色。

LDA的主要特点如下：

1. 监督学习：LDA是一种监督学习方法，它需要利用标签信息来训练模型。
2. 线性投影：LDA通过寻找特征空间中的线性组合，将数据投影到低维空间。
3. 最大化类间方差和最小化类内方差：LDA的目标是最大化不同类别之间的分离度，同时最小化同一类别内部的差异。
4. 适用于高维数据：LDA可以有效地处理高维数据，通过降维来降低计算复杂度。
5. 分类和降维双重功能：LDA不仅可以用于分类，还可以用于降维。

LDA在线性模型中具有重要的地位，它结合了降维和分类的优点，是一种非常实用的算法。

然而，LDA也有一些局限性，例如它假设数据服从正态分布，并且类内方差相等。

在实际应用中，我们需要根据数据的特点选择合适的算法。