洛谷 P1886 滑动窗口(单调队列)

题目链接

https://www.luogu.org/problemnew/show/P1886

题目描述

现在有一堆数字共N个数字（N<=10^6），以及一个大小为k的窗口。现在这个从左边开始向右滑动，每次滑动一个单位，求出每次滑动后窗口中的最大值和最小值。

例如：

The array is [1 3 -1 -3 5 3 6 7], and k = 3.

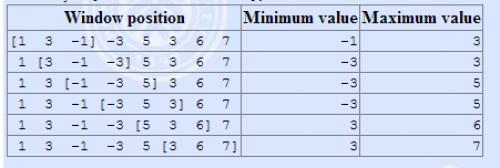
输入输出格式

输入格式：

输入一共有两行，第一行为n,k。

第二行为n个数(<INT_MAX).

输出格式：

输出共两行，第一行为每次窗口滑动的最小值

第二行为每次窗口滑动的最大值

输入输出样例

输入样例#1：

8 3
1 3 -1 -3 5 3 6 7

输出样例#1：

-1 -3 -3 -3 3 3
3 3 5 5 6 7

说明

50%的数据，n<=10^5

100%的数据，n<=10^6

解题思路

先理解文意：对于给定一个长度为n的序列，找出所有长为k的区间的最大值（最小值）。

首先很多人会想到，枚举每一个长为k的区间，然后遍历一遍，找到最大值（最小值），这样的时间复杂度是o(nk)的，显然超时。

所以我们需要换一种思路。

单调队列：单调队列就是一个一直保持单调性(递增或递减)的长度最大为k的双端队列。

我们维护这样一个单调队列，使它队首元素即为要求的最大值（最小值）。

所以本题的核心是：怎样维护一个单调队列。

在此举例求最大值：对于任意读入的元素，我们不放设为in，首先判断队列是否为空，如果队列为空，就一定要加入队列。若不为空，就一直比较队列末尾的元素，不放设为f，如果f<in，就把f弹出去，砍掉。为什么呢？因为f能做到的，in一定也能做到，in>f，所以在一定范围内，答案有可能是in，但永远不可能是f。（这里有一个有趣的类比，如果一位OIer比你年轻还比你强，那你就没法超越他了。——Kevin大佬）。还有一个问题，就是滑动窗口长度最大是k，所以我们需要用结构体保存每一个数的编号和数值，如果in的编号和队首的编号的差>=k，就把队首砍掉，这是显然的。

这样，由于每一个元素只进入队列一次，所以时间复杂度就变成o(n)了。

话不多说，看代码。

 #include<iostream>
 #include<cmath>
 #include<cstdio>
 #include<cstring>
 #include<string>
 #include<cstdlib>
 #include<queue>
 #include<set>
 #include<map>
 #include<vector>
 #include<algorithm>
 #include<iomanip>
 #include<ctime>                            //还是写了一大堆没用的头文件
 using namespace std;
 int n,k;
 int maxx[],minn[];        //由于输出要求，需要先用数组存好答案
 struct num{                                //结构体储存编号和数值
     int cnt,value;
     num(int a,int b):cnt(a),value(b){}  //结构体构造函数，作用是在定义结构体的时候，就会给cnt和value赋值。用法具体看29行或者39行代码
 };
 deque<num> q1,q2;                         //定义两个双端队列，q1储存最大值，q2储存最小值
 void makeq1(int i,int in){                //makeq1处理最大值
     if(q1.empty()) q1.push_back(num(i,in));//队列为空时直接入队
     else{
         num f=q1.front();
         if(i>f.cnt+k-) q1.pop_front();//判断队列长度是否超过k
         if(!q1.empty()){                //队尾弹不断弹出操作
             num b=q1.back();
             while(b.value<in){
                 q1.pop_back();
                 if(q1.empty()) break;
                 b=q1.back();
             }
         }
         q1.push_back(num(i, in));
     }
 }
 void makeq2(int i,int in){                //makeq2处理最小值
     if(q2.empty()) q2.push_back(num(i,in));//队列为空时直接入队
     else{
         num f=q2.front();
         if(i>f.cnt+k-) q2.pop_front();        //判断队列长度是否超过k
         if(!q2.empty()){                    //队尾弹不断弹出操作
             num b=q2.back();
             while(b.value>in){                //和makeq1不同的地方
                 q2.pop_back();
                 if(q2.empty()) break;
                 b=q2.back();
             }
         }
         q2.push_back(num(i, in));
     }
 }
 int main()
 {
 cin>>n>>k;
 for(int i=;i<=n;i++){
     int in;
     cin>>in;
     makeq1(i,in);
     makeq2(i,in);
     if(i>=k){                                //如果长度达到k，就储存结果
         maxx[i]=q1.front().value;
         minn[i]=q2.front().value;
     }
 }
 for(int i=k;i<=n;i++) cout<<minn[i]<<" ";    //注意输出格式
 cout<<endl;
 for(int i=k;i<=n;i++) cout<<maxx[i]<<" ";
 return ;
 }

AC代码