P2239 螺旋矩阵

P2239 螺旋矩阵

题解

这题看上去是个暴力，但是你看数据范围啊，暴力会炸

实际上这是一道数学题QWQ

先看看螺旋矩阵是个什么亚子吧

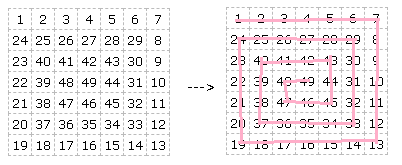
好吧，找找规律

1	2	...	...	...	...	...	n
4(n-1)	4(n-1)+1					4(n-1)+n	n+1
...							...
							...
							...
...							...
...	4(n-1)+(3n-2)					4(n-1)+(2n-1)	...
3n-2	...					...	2n-1

这个矩阵可以划分成一圈一圈的亚子

所以就可以像剥洋葱一样一层一层的处理

如果这个位置在边界（也就是在圈上），找规律直接求解

如果在内部的话，我们就剥去一层，寻找下一层，反正总会到头的啊

注意一下:

剥去一层，n的规模就 -2 ，下一层统一比上一层小 4(n-1)

代码

#include<bits/stdc++.h>

using namespace std;

int n,x,y;

int dfs(int n,int i,int j)
{
    if(i==) return j;
    if(j==) return *n--i;
    if(j==n) return n+i-;
    if(i==n) return *n--j;
    else return dfs(n-,i-,j-)+*(n-);
}

int main()
{
    scanf("%d%d%d",&n,&x,&y);
    int ans;
    ans=dfs(n,x,y);
    printf("%d",ans);
    return ;
}