[洛谷P4436] HNOI/AHOI2018 游戏

问题描述

一次小G和小H在玩寻宝游戏，有n个房间排成一列，编号为1,2,...,n，相邻的房间之间都有一道门。其中一部分门上锁（因此需要有对应的钥匙才能开门），其余的门都能直接打开。现在小G告诉了小H每把锁的钥匙在哪个房间里（每把锁有且只有一把钥匙与之对应），并作出p次指示：第i次让小H从第\(S_i\)个房间出发到\(T_i\)个房间里。但是小G有时会故意在指令中放入死路，而小H也不想浪费多余的体力去尝试，于是想事先调查清楚每次的指令是否会存在一条通路。

你是否能为小H作出解答呢？

输入格式

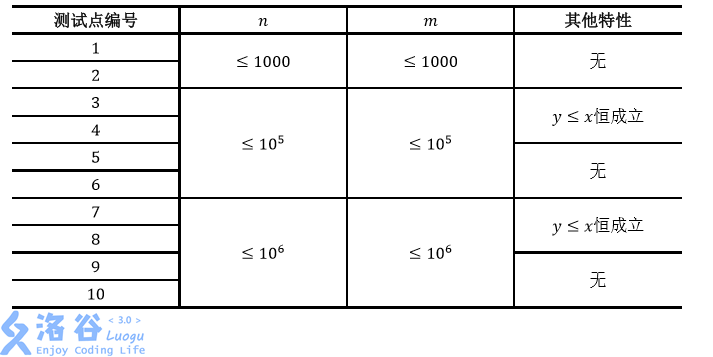
第一行三个数字：n,m,p，代表有n个房间，m道门上了锁，以及p个询问。接下来m行，每行两个数字x,y代表x到x+1的钥匙在房间y。接下来p行，其中第i行是两个整数\(S_i,T_i\)，代表一次询问。

输出格式

输出p行，每行一个“YES”或"NO"，分别代表能或不能到达。

样例输入

5 4 5

1 3

2 2

3 1

4 4

2 5

3 5

4 5

2 1

3 1

样例输出

YES

NO

YES

YES

NO

说明

解析

可以发现对于每个点i，最后能到达的区域一定是一段区间[Li,Ri]。那么问题就是如何求这些区间。

如果一扇门的钥匙在这扇门的左边，那么就不能从右边穿过这扇门；如果在这扇门的右边，就不能从左边穿过去。那么，如果我们对每扇门的两边，由不能到达的向能到达的连边，可以发现一个点的区间范围一定可以由拓扑序在这个点前面的点得到(只有前面的点有边连向这个点)。所以，可以利用拓扑排序，对队首的点，向左向右扩展，扩展的点注意门的编号等于门右边的编号减一，具体见代码。

但是，对于一个可以互达的区间，有可能会连成一个环，这样拓扑排序就没有意义了。所以，最开始需要预处理能够互达的区间，并将这个区间缩成一个点。同时将所有信息更新成缩点之后的。

回答询问时，只需判断T是否在S的可达区间中即可。

代码

#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#define N 1000002
#define M 1000002
using namespace std;
int head[N],ver[M],nxt[M],d[N],t;
int n,m,q,i,x[N],y[N],pos[N],cnt=1,gap[N],l[N],r[N];
bool lock[N];
int read()
{
	char c=getchar();
	int w=0;
	while(c<'0'||c>'9') c=getchar();
	while(c<='9'&&c>='0'){
		w=w*10+c-'0';
		c=getchar();
	}
	return w;
}
void insert(int x,int y)
{
	t++;
	ver[t]=y;
	nxt[t]=head[x];
	head[x]=t;
	d[y]++;
}
bool check(int x,int y)
{
	if(y==0||y==cnt+1) return 0;
	if(x<y) y--;
	return l[x]<=pos[y]&&pos[y]<=r[x];//钥匙是否在当前可达区间中
}
void toposort()
{
	queue<int> q;
	for(int i=1;i<=cnt;i++){
		if(d[i]==0) q.push(i);
	}
	while(!q.empty()){
		int x=q.front();
		q.pop();
		bool flag=1;
		while(flag){
			flag=0;
			while(check(x,l[x]-1)) l[x]=l[l[x]-1],flag=1;//可以就更新为左边的左端点
			while(check(x,r[x]+1)) r[x]=r[r[x]+1],flag=1;//更新为右边的右端点
		}
		for(int i=head[x];i;i=nxt[i]){
			int y=ver[i];
			d[y]--;
			if(d[y]==0) q.push(y);
		}
	}
}
int main()
{
	n=read();m=read();q=read();
	for(i=1;i<=m;i++){
		x[i]=read();y[i]=read();
		lock[x[i]]=1;
	}
	lock[n]=1;
	for(i=1;i<=n;i++){
		gap[i]=cnt;
		if(lock[i]){
			l[cnt]=r[cnt]=cnt;
			cnt++;
		}
	}
	cnt--;
	for(i=1;i<=m;i++){
		int tx=gap[x[i]],ty=gap[y[i]];
		pos[tx]=ty;
		if(ty<=tx) insert(tx+1,tx);
		else insert(tx,tx+1);
	}
	toposort();
	for(i=1;i<=q;i++){
		int x=read(),y=read();
		x=gap[x],y=gap[y];
		if(l[x]<=y&&y<=r[x]) puts("YES");
		else puts("NO");
	}
	return 0;
}