Dijkstra算法解决单源最短路径

单源最短路径问题:给定一个带权有向图 G = (V, E), 其中每条边的权是一个实数.另外,还给定 V 中的一个顶点,称为源.现在要计算从源到其他所有各顶点的最短路径长度.这里的长度是指路上各边权之和.这个问题通常称为单源最短路径问题.

Dijkstra算法:

一:基本算法

将图 G 中所有的顶点 V 分成两个顶点集合 V_A 和 V_B.如果源点 S 到 u 的最短路径已经确定,则点 u 属于集合 V_A ,否则属于集合  V_B.最开始的时候 V_A 只包含源点 S,其余的点属于 V_B,算法结束时所有由源点 S 可达的点属于  V_A ,由源点 S 不可达的点仍留在 V_B 中.可以在求出最短路径长的同时记录最短路径,方法是距离终点的前一个点,这样只要倒着往回查就能确定整条最短路径.算法的适用范围是权值非负的图,即解决带有非负权值的图中的单源最短路径问题.

二:具体步骤

　　(1):首先初始化,将源点 S 到图中各点的直接距离当做初始值记录为 S 到各点的最短距离,如果不能直接到达,记为 INF, S 到 S 的距离为 0.

　　(2):在所有属于 V_B 的点中找一个 S 到其路径长度最短的点 u, 将 u 从V_B 中除去,加入到 V_A 中,即当前求出的从 S 到 u 的路径为 S 到 u 的最短路径.

　　(3):由新确定的 u 点更新 S 到 V_B 中每一点 v 的距离, 如果 S 到 u 的距离加上 u 到 v 的直接距离小于当前 S 到 v 的距离,表明新生成的最短路径的长度要比前面计算的更短,那么就更新这个距离,同时更新最短路径.

　　(4):重复(2),(3)步骤,直到V_B 中已经没有剩余的点或者V_B 中的点都不能由源点 S 到达为止.

三:伪代码

　　在这里, s 代表源, setA[] 记录点属于哪个集合: true 表示属于V_A , false 表示属于V_B ; map[][] 记录图的信息, map[u][v]为点 u 到点 v 的边的长度, 结果保存在 dist[]中,pre[]记录最短路径终点的前趋.

　　(1):初始化:源的距离 dist[s] 设为0,其他的点距离设为 map[s][i],即 dist[i] = map[s][i].setA[s]设为 true,其他各点的p[i] = false.

(2):循环 n - 1次:

a:在 V_B 中的点中取一 s 到其距离最小的点 k, setA[k] = true. 如果所有的 k 都不可达,退出循环,算法结束.

b:对于每个与 k 相邻且在 V_B 中的点 j,更新 s 到 j 的最短路径. 如果 dist[k] + map[k][j] < dist[j], 那么 dist[j] = dist[k] + map[k][j], 此时到点 j 的最短路径上, 终点 j 的前一个节点即为 k, 即 pre[j] = k.

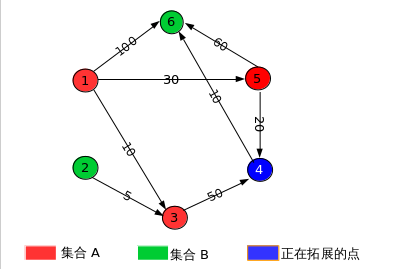
四:以图为例

初始化图:

初始化数组:

dist        1        2        3         4         5         6

0        INF    10        INF     30       100

setA       1        2        3         4         5         6

1        0        0         0         0         0

第一步:

从 dist 数组中选择属于集合 B 且与 点“1” 距离最短的点,显然是点 “3”, 把点 “3” 加入集合 A.则改变后的图为:

然后选择与点 “3” 相邻的点且属于集合 B 的点,只有点 4,选择之后更新:

dist[4](INF) < dist[3](10) + map[3][4](50) 显然这里是成立的, 则dist[4] = dist[3] + map[3][4] = 60,更新后的数组为:

dist     1     2     3     4     5     6

0    INF   10   60  30  100

setA   1     2     3      4      5     6

1     0     1      0     0      0

第二步:

再次从 dist 数组中选择属于集合 B 且距离 源点 “1” 最短的点,可以看出这次拓展的点是点 “5”,把点 “5”加入集合A,图变为:

选择与点 “5” 相邻的点且属于集合 B 的点,这里有点 “4” 和点 “6”.则做比较更新:

点“4”: dist[4](60) < dist[5](30) + map[5][4](20)  这里是成立的,则dist[4] = dist[5](30) + map[5][4](20) = 50;

点“6”: dist[6] < dist[5](30) + map[5][6](60) 这也是成立的,则 dist[6] = dist[5] + map[5][6] = 90;

更新数组得:

dist     1     2     3     4     5     6

0    INF   10   50  30   90

setA   1     2     3      4      5     6

1     0     1      0      1     0

第三步:

再次选择符合条件的点,可知下一个待扩展点为点 “4”.

同样选择与点“4”相邻且属于集合B的点,可选点为 点 “6”.对点 “6”做更新:

dist[6](90) < dist[4](50) + map[4][6](10) 这里也是成立的,那么dist[6] = dist[4] + map[4][6] = 60. 更新后的数组为.

dist     1     2     3     4     5     6

0    INF   10   50  30   60

setA   1     2     3      4      5     6

1     0     1      1      1     0

第四步:

继续再集合B中选择距离源点最短的点,可得点 “6”.

由于此时已经没有和点 “6”相邻,且属于集合B的点了.那么把点 “6” 加入集合A继续下一步.

dist     1     2     3     4     5     6

0    INF   10   50  30   60

setA   1     2     3      4      5     6

1     0     1      1      1     1

第五步:

此时满足距离源点最短且属于集合B的点不存在,即剩下的属于集合B的点,已不可到达那么此时算法结束:

算法结束后,dist数组里保存的就是图中每点到源点的最短距离:

dist      1      2      3      4      5      6

0      INF  10    50    30    60

其中点 “2”为 不可到达.

五:代码

 const int INF = INT_MAX;
 const int MAXN =;
 int mmap[MAXN + ][MAXN + ];//记录图的信息
 int dist[MAXN + ];//dist[i]表示点 i 到源点的最短距离
 int pre[MAXN + ];//记录前趋 记录最短路径
 bool setA[MAXN + ];//是否属于集合A,集合A代表着已经确定最短路径的点集

 void Dijkstra(int n, int s) {// s 为源点
     for(int i = ; i <= n; i++) { //初始化
         setA[i] = false;
         if(i != s) {
             dist[i] = mmap[s][i];
             pre[i] = s;
         }
     }
     dist[s] = , setA[s] = true;
     for(int i = ; i <= n - ; i++) {//求 s 到其他 n - 1个节点的最短路径
         int minn = INF;
         int k = ;
         for(int j = ; j <= n; j++) { // 在属于集合 Vb 的点中取一点, 满足 s 到其的距离最小
             if(!setA[j] && dist[j] < minn) {
                 minn = dist[j], k = j;
             }
         }
         if(!k) return; // 没有点可以扩展,即剩余的点不可达,则结束算法
         setA[k] = true; //将新找的点从集合 Vb 中除去, 加入集合 Va
         for(int j = ; j <= n; j++) {
             //对于每个与 k 相邻 且属于 Vb 的点,更新 s 到 j 的最短路径
             if(!setA[j] && mmap[k][j] != INF && dist[j] > dist[k] + mmap[k][j]) {
                 dist[j] = dist[k] + mmap[k][j];
                 pre[j] = k;
             }
         }
     }
 }

参考文献:<<图论及应用>>  <<数据结构>>