【计数】hdu5921Binary Indexed Tree

二进制拆位计算贡献

题目描述

树状数组是一种常用的数据结构，下面是树状数组用于给区间 [1,x] 内的数加 t 的代码：

 void add(int x,int t){
     for (int i=x;i;i-=(i&(-i))){
         cnt[i]+=t;
     }
 }

当你要给 [l,r] 区间加 x 时，肯定是先给 [1,l−1] 加 −x，然后给 [1,r] 加 x

令 f(l,r) 为：在 cnt 数组一开始为 0 的情况下给区间[l,r]区间加1后，cnt 数组有多少位置不为0。

现在给定 n，求  \sum_{l=1}^{n} \sum_{r=1}^{n} f(l,r)，对1e9+7取模

输入格式

第一行 T

T 行， 一个 n

输出格式

T 行答案

数据范围

1≤n≤10^18,1≤T≤10^4

---

题目分析

这题主流做法是数位dp。不过从hdu5921Binary Indexed Tree学习到一种拆位算贡献的方法

（但是请注意！上面引用的这篇博客关于f(i),g(i)的分析有写错的地方！）

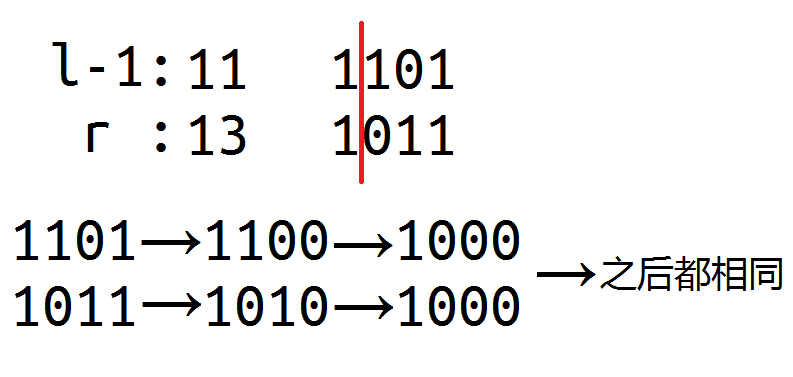
本题树状数组求的是后缀和；而∑f(l,r)求的是l-1和r这两个数在依次减去lowbit的过程中不同的数的个数：那么只有当l-1和r变成lcp(l-1,r)时，接下去的数才会相同。

记g(i)为i二进制中1的个数，所求即

（公式崩了只能用图片）

经过上面分析之后，问题相当于转变为求∑g(i)和Σg(lcp(l-1,r))。由于数据范围是10^18级别，显然我们需要log算法。

将n二进制拆位，考虑从右往左第$i$位的贡献。记[i+1...lens]在十进制下为nxt[i+1]，[1...i-1]在十进制下为pre[i-1]。

1.计算gi第一步：左边的数不改变

那么为了不大于原数，右边的数应取0...pre[i-1]。

当ai==1时，有pre[i-1]+1的贡献

2.计算gi第二步：左边的数可改变

与上一种情况相对应，左边的数应取0...nxt[i+1]-1.那么此时右边的数可以任意取值，有2^i种取值。

所以这种情况下，无论ai取值如何，都有nxt[i+1]*2^i的贡献。

至于还要处理两两lcp的部分，则与之类似。由于是数对之间的负贡献，算的时候再多乘上去就好了。

 #include<bits/stdc++.h>
 typedef long long ll;
 const ll MO = ;

 int T,bin[],lens;
 ll n,ans,power[],pre[],nxt[];

 ll read()
 {
     char ch = getchar();
     ll num = ;
     bool fl = ;
     for (; !isdigit(ch); ch=getchar())
         if (ch=='-') fl = ;
     for (; isdigit(ch); ch=getchar())
         num = (num<<)+(num<<)+ch-;
     if (fl) num = -num;
     return num;
 }
 int main()
 {
     T = read(), power[] = ;
     for (int i=; i<=; i++) power[i] = (power[i-]<<)%MO;
     while (T--)
     {
         n = read(), ans = lens = ;
         for (ll x=n; x; x>>=) bin[++lens] = x&;
         pre[] = nxt[lens+] = ;
         for (int i=; i<=lens; i++) pre[i] = (pre[i-]+power[i-]*bin[i])%MO;
         for (int i=lens; i>=; i--) nxt[i] = ((nxt[i+]<<)+bin[i])%MO;
         for (int i=; i<=lens; i++)
         {
             if (bin[i]) pre[i-]++, ans = (ans+pre[i-])%MO;
             ans = (ans+nxt[i+]*power[i-]%MO)%MO;
         }
         ans = (n+1ll)%MO*ans%MO;
         for (int i=; i<=lens; i++)
         {
             if (bin[i]) ans = (ans+MO-pre[i-]*pre[i-]%MO)%MO;
             ans = (ans-nxt[i+]*power[i-]%MO*power[i-]%MO+MO)%MO;
         }
         printf("%lld\n",ans);
     }
     return ;
 }

END