UVA10870 Recurrences —— 矩阵快速幂

题目链接：https://vjudge.net/problem/UVA-10870

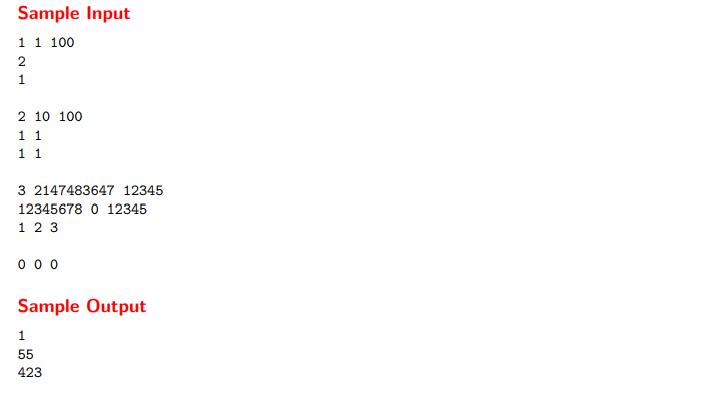
题意：

典型的矩阵快速幂的运用。比一般的斐波那契数推导式多了几项而已。

代码如下：

 #include <bits/stdc++.h>
 #define rep(i,s,t) for(int (i)=(s); (i)<=(t); (i)++)
 #define ms(a,b) memset((a),(b),sizeof((a)))
 using namespace std;
 typedef long long LL;
 const int INF = 2e9;
 const LL LNF = 9e18;
 const double eps = 1e-;
 const int mod = ;
 const int maxn = 2e5+;

 struct MA
 {
     LL mat[][];
     void init()
     {
         rep(i,,) rep(j,,)
             mat[i][j] = (i==j);
     }
 };

 LL n,d,m;
 LL a[],f[];

 MA mul(MA x, MA y)
 {
     MA tmp;
     ms(tmp.mat,);
     rep(i,,d) rep(j,,d) rep(k,,d)
         tmp.mat[i][j] += (1LL*x.mat[i][k]*y.mat[k][j])%m, tmp.mat[i][j] %= m;
     return tmp;
 }

 MA qpow(MA x, LL y)
 {
     MA s;
     s.init();
     while(y)
     {
         if(y&) s = mul(s,x);
         x = mul(x,x);
         y >>= ;
     }
     return s;
 }

 int main()
 {
     while(scanf("%lld%lld%lld",&d,&n,&m) && (d || n||m))
     {
         rep(i,,d) scanf("%lld",&a[i]);
         rep(i,,d) scanf("%lld",&f[i]);

         if(n<=d)
         {
             printf("%lld\n", f[n]);
             continue;
         }

         MA x;
         ms(x.mat,);
         rep(i,,d) x.mat[][i] = a[i];
         rep(i,,d) x.mat[i][i-] = ;
         x = qpow(x,n-d);

         LL ans = ;
         rep(i,,d)
             ans += (1LL*x.mat[][i]*f[d-i+])%m, ans %= m;
         printf("%lld\n",ans);
     }
 }