hdu3739 Anti LIS[最小割]

长度为 n≤1000 的数列 ai，其中最长上升子序列的长度为 s。至少删去多少数使得最长上升子序列的长度小于 s。

---

其实这题和那个求有多少不重叠LIS是一样答案的.

先放个图。

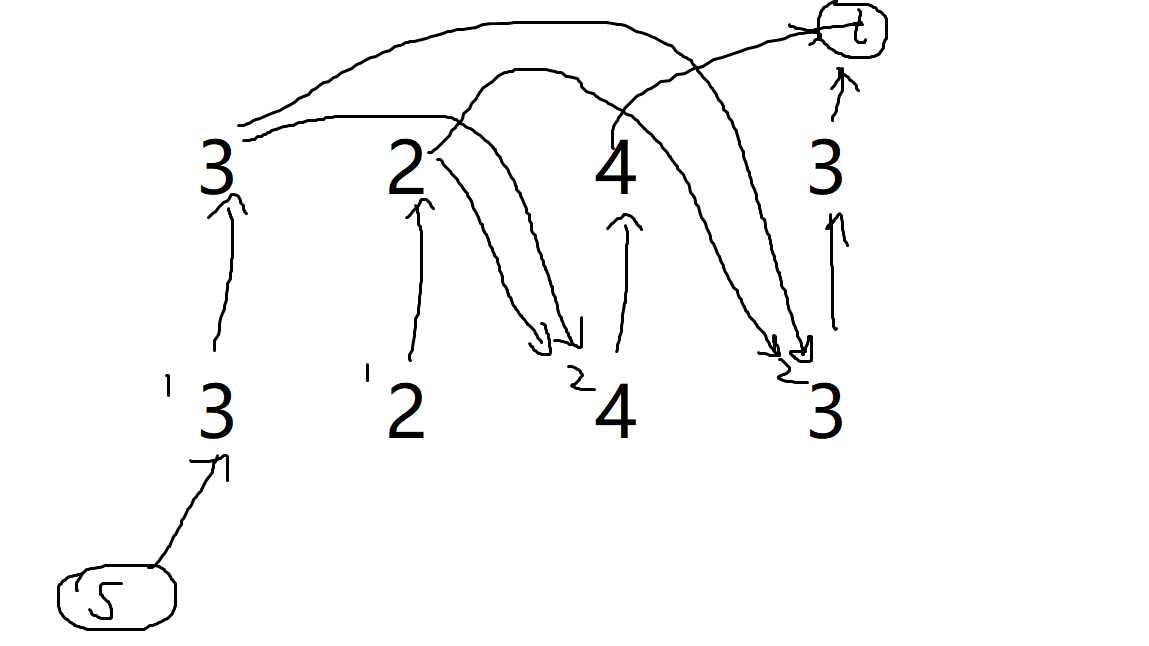
图丑别说我。

原网络的意思是从s到t是一条lis,那我们就对这个图进行破坏，求出一个最小割使它不连通即可。这里有几个问题。为什么是最小割？可以看出，删数操作就相当于把那个拆点间的边删掉，并且这种删法是最优的（看图想一想），比删入度，出度价值更少。那么就可以把删数想象为求最小割即最大流啦。最小割去掉后的数列不会再出现一个长s的lis吗？不会的，如果有，那删之前应该也是存在的，那就应该被删掉，与现在又出现矛盾，故不会出现。

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 typedef pair<int,int> pii;
 template<typename T>inline char MIN(T&A,T B){return A>B?A=B,:;}
 template<typename T>inline char MAX(T&A,T B){return A<B?A=B,:;}
 template<typename T>inline T _min(T A,T B){return A<B?A:B;}
 template<typename T>inline T _max(T A,T B){return A>B?A:B;}
 template<typename T>inline T read(T&x){
     x=;char c;while(!isdigit(c=getchar()))if(isalpha(c))return x=(int)c;
     while(isdigit(c))x=(x<<)+(x<<)+(c^),c=getchar();return x;
 }
 const int N=+,M=+,INF=0x3f3f3f3f;
 int w[M<<],v[M<<],Next[M<<],Head[N<<],cur[N<<],dis[N<<],tot,s,t,n;
 inline void Addedge(int x,int y,int z){
     v[++tot]=y,Next[tot]=Head[x],Head[x]=tot,w[tot]=z;
     v[++tot]=x,Next[tot]=Head[y],Head[y]=tot,w[tot]=;
 }
 #define y v[j]
 inline char bfs(){
     queue<int> q;q.push(s),memset(dis,,sizeof dis),dis[s]=;
     for(register int i=;i<=(n<<)+;++i)cur[i]=Head[i];
     while(!q.empty()){
         int x=q.front();q.pop();
         for(register int j=Head[x];j;j=Next[j])if(w[j]&&!dis[y]){
             dis[y]=dis[x]+,q.push(y);
             if(y==t)return ;
         }
     }
     return ;
 }
 int dinic(int x,int flow){
     if(!flow||x==t)return flow;
     int rest=flow,k;
     for(register int j=cur[x];j&&rest;cur[x]=j,j=Next[j])if(w[j]&&dis[y]==dis[x]+){
         if(!(k=dinic(y,_min(rest,w[j]))))dis[y]=;
         rest-=k,w[j]-=k,w[j^]+=k;
     }
     return flow-rest;
 }
 #undef y
 int a[N],f[N],ans,maxflow,T;

 int main(){//freopen("P2766.in","r",stdin);//freopen("P2766.txt","w",stdout);
     read(T);while(T--){
         tot=;read(n);s=(n<<)+,t=s+,ans=maxflow=;
         memset(Head,,sizeof Head);
         for(register int i=;i<=n;++i){
             read(a[i]);f[i]=;
             for(register int j=;j<i;++j)if(a[j]<a[i])MAX(f[i],f[j]+);
             for(register int j=;j<i;++j)if(a[j]<a[i]&&f[j]+==f[i])Addedge(j+n,i,);
             MAX(ans,f[i]);Addedge(i,i+n,);if(f[i]==)Addedge(s,i,);
         }
         for(register int i=;i<=n;++i)if(f[i]==ans)Addedge(i+n,t,);
         while(bfs())maxflow+=dinic(s,INF);
         printf("%d\n",maxflow);
     }
     return ;
 }