leecode第四题（寻找两个有序数组的中位数）

题解:

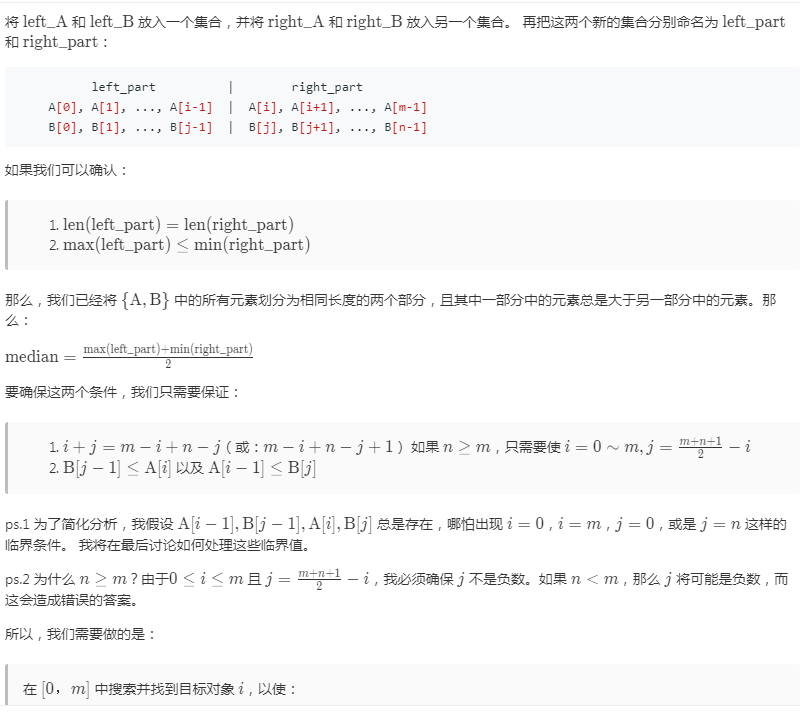
class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        int m = nums1.size();
        int n = nums2.size();
        if (m > n) return findMedianSortedArrays(nums2, nums1);//保证nums1个数少于nums2
        int iMin = , iMax = m, halfLen = (m + n + ) / ;
        while (iMin <= iMax) {
            int i = (iMin + iMax) / ;
            int j = halfLen - i;//保证左右部分数目一样多
            if (i < iMax && nums2[j - ] > nums1[i]) {
                iMin = i + ; // i is too small
            }
            else if (i > iMin && nums1[i - ] > nums2[j]) {
                iMax = i - ; // i is too big
            }
            else { // i is perfect，这里满足左部分最大点小于等于右部分最小点
                int maxLeft = ;
                if (i == ) { maxLeft = nums2[j - ]; }
                else if (j == ) { maxLeft = nums1[i - ]; }
                else { maxLeft = max(nums1[i - ], nums2[j - ]); }//这些都是极值情况，放在最后输出处理即可
                if ((m + n) %  == ) { return maxLeft; }

                int minRight = ;
                if (i == m) { minRight = nums2[j]; }
                else if (j == n) { minRight = nums1[i]; }
                else { minRight = min(nums2[j], nums1[i]); }

                return (maxLeft + minRight) / 2.0;//偶数个的中位数
            }
        }
        return 0.0;
    }
};

总结：

我很惭愧，这个题写了三个多小时都没做出来，我一开始看到时间复杂度，想到二分法，然后不停判断并删除两个数组中大于中位数的值，然后稳定条件是两个数组剩余个数是m+n的一半，程序就是有问题。。。

总得来说还是没有洞悉最有价值的规律，分析情况又把我绕迷糊了，唉，学习到了。