MapReduce实现与自定义词典文件基于hanLP的中文分词详解

前言：

文本分类任务的第1步，就是对语料进行分词。在单机模式下，可以选择python jieba分词，使用起来较方便。但是如果希望在Hadoop集群上通过mapreduce程序来进行分词，则hanLP更加胜任。

一、使用介绍

hanLP是一个用java语言开发的分词工具， 官网是 http://hanlp.com/ 。 hanLP创建者提供了两种使用方式，一种是portable简化版本，内置了数据包以及词典文件，可通过maven来管理依赖，只要在创建的 maven 工程中加入以下依赖，即可轻松使用（强烈建议大家优先采用这种方法）。

具体操作方法如图示，在pom.xml中，加入上述依赖信息，笔者使用的IDEA编辑器就会自动开始解析依赖关系，并导入左下角的hanlp jar包。

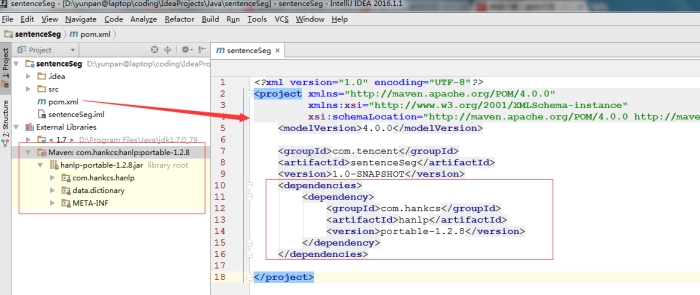
第二种方法需要自己下载data数据文件，并通过一个配置文件hanlp.properties来管理各种依赖信息，其中最重要的是要人为指定data目录的家目录。（不建议大家一上来就使用这种方法，因为真心繁琐！）

二、通过第一种方法，建立maven工程，编写mapreduce完整程序如下（亲测运行良好）：

三、添加自定义词典文件 & 单机模式

有时候我们希望根据自己业务领域的一些专有词汇进行分词，而这些词汇可能并不包含在官方jar包自带的分词词典中，故而我们希望提供自己的词典文件。首先，我们定义一个测试的句子，并用系统默认的词典进行分词，可看到效果如下图所示：

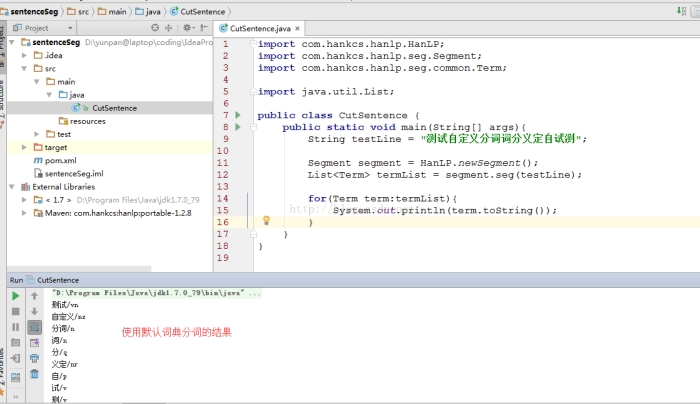
假设在我们的专业领域中，“词分”，“自试” 都是专业术语，那么使用默认词典就无法将这些目标词分出来了。这时就要研究如何指定自定义的词典，并在代码中进行调用。这时有2种方法。

1. 在代码中，通过CustomDictionary.add();来添加自己的词汇，如下图所示, 可以看到这次分词的结果中，已经能将“词分”，“自试” 单独分出来了。

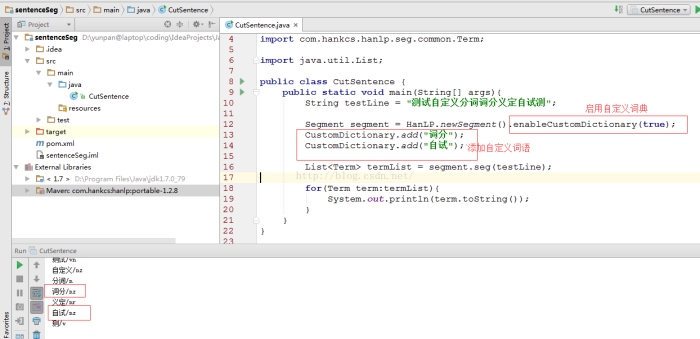
假如说我们想添加的词汇较多呢，通过上面的方法，一个一个 add, 未勉显得不够优雅，这时我们就希望通过一个词典文件的形式来添加自定义词汇。在官方网站上，提供了如下一种方法。该方法要求我们单独下载一个data目录，以及定义一个配置文件。下面我们就来看下如何操作。

首先，下载好上面的hanlp.jar后，在java工程师导入该包。同时在src目录下创建一个hanlp.properties配置文件，内容直接复制官网上的内容，但是注意修改两个地方。

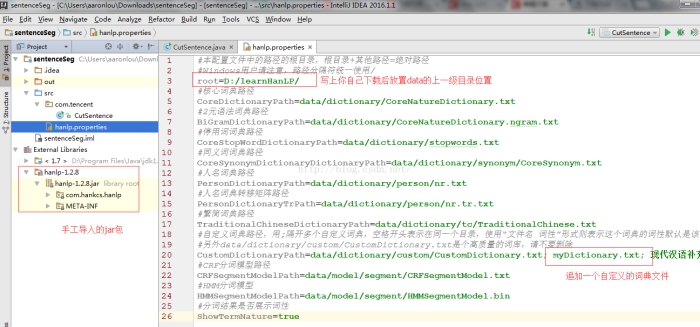
其中myDictionary.txt是我们自己创建的一个词典文件，其内容为：

这时候，再运行方法1同样的代码，可看到如下结果中，也将“词分”、“自试” 分了出来。

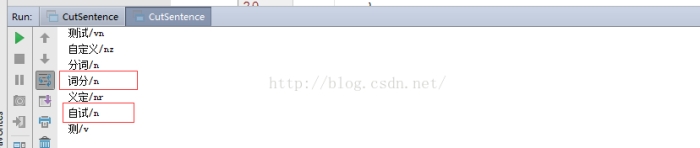
注意，如果你不想显示/n /nr这样的记性，也可以将上述配置文件中最后一行

ShowTermNature=true

修改为

ShowTermNature=false

注意，这时候，运行成功的话，会在词典目录下生成一个词典缓存文件

四、自定义词典文件 & mapreduce提交

写到这里，想必细心的人已经想到了，当我们希望将编辑好的mapreduce程序打成jar包，提交到集群上运行时，上面这种通过配置文件指定data目录的方法还可行吗？ 反正我是没有搞定。理论上，要么我们需要把data上传到集群上每个节点，要么把data直接打到jar包中。但是，这两种方法本人尝试都没有成功。最终，跟一位同事相互讨论后，借鉴了对方的方法。即我们猜想，portable版本自带了data数据，且不需要额外指定配置文件。而我们现在想做的就是添加了一些自定义词汇，那么，是否我们将其中的词典缓存文件替换掉，就行了呢？动手试下才知道嘛。这次不通过maven来管理依赖，直接下载portable版本的jar包，然后打开压缩文件，删除data\dictionary\custom目录下的CustomDictionary.txt.bin文件，然后将上一步运行成功的CustomDictionary.txt.bin粘贴进去！ 将工程打成jar包，再通过命令行进入其所在目录，执行java -jar  包名， 发现可以执行成功。然后，为了测试是否对这个绝对路径有依赖，我们故意将该jar包剪切到 d:\ ， 再执行一下，发现同样是成功的。

具体到提交到集群上运行，我们就不赘述了。这个方法虽然土一些，但至少是可用的。

文章转载自 a_step_further 的博客（有小幅改遍）