magic矩阵 分类: 数学 2015-07-31 22:56 2人阅读 评论(0) 收藏
魔方矩阵
魔方矩阵是有相同的行数和列数,并在每行每列、对角线上的和都相等。你能构造任何大小(除了2x2)的魔方矩阵。
1.历史
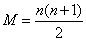
2.魔方构造
N 为奇数时
N为4的倍数时
N 为其它偶数时
3.算法设计
4.魔方函数
magic(5) ,将随机产生5阶魔方阵。
|
1
2
3
4
5
6
7
8
|
>> magic(4)ans = 16 5 9 4 |
版权声明:本文为博主原创文章,未经博主允许不得转载。
magic矩阵 分类: 数学 2015-07-31 22:56 2人阅读 评论(0) 收藏的更多相关文章
- C/C++文字常量与常变量的概念与区别 分类: C/C++ 2015-06-10 22:56 111人阅读 评论(0) 收藏
以下代码使用平台是Windows 64bits+VS2012. 在C/C++编程时,经常遇到以下几个概念:常量.文字常量.符号常量.字面常量.常变量.字符串常量和字符常量,网上博客资料也是千篇千律,不 ...
- 全方位分析Objcetive-C Runtime 分类: ios技术 2015-03-11 22:29 77人阅读 评论(0) 收藏
本文详细整理了 Cocoa 的 Runtime 系统的知识,它使得 Objective-C 如虎添翼,具备了灵活的动态特性,使这门古老的语言焕发生机.主要内容如下: 引言 简介 与Runtime交互 ...
- 快速幂取模 分类: ACM TYPE 2014-08-29 22:01 95人阅读 评论(0) 收藏
#include<stdio.h> #include<stdlib.h> //快速幂算法,数论二分 long long powermod(int a,int b, int c) ...
- Digital Roots 分类: HDU 2015-06-19 22:56 13人阅读 评论(0) 收藏
Digital Roots Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) Total ...
- Hibernate检索方式 分类: SSH框架 2015-07-10 22:10 4人阅读 评论(0) 收藏
我们在项目应用中对数据进行最多的操作就是查询,数据的查询在所有ORM框架中也占有极其重要的地位.那么,如何利用Hibernate查询数据呢?Hibernate为我们提供了多种数据查询的方式,又称为Hi ...
- Red and Black(BFS or DFS) 分类: dfs bfs 2015-07-05 22:52 2人阅读 评论(0) 收藏
Description There is a rectangular room, covered with square tiles. Each tile is colored either red ...
- IOS之富文本编辑 分类: ios技术 2015-03-06 22:51 89人阅读 评论(0) 收藏
之前做项目时遇到一个问题: 使用UITextView显示一段电影的简介,由于字数比较多,所以字体设置的很小,行间距和段间距也很小,一大段文字挤在一起看起来很别扭,想要把行间距调大,结 ...
- 【从0到1学Web前端】CSS伪类和伪元素 分类: HTML+CSS 2015-06-02 22:29 1065人阅读 评论(0) 收藏
1.CSS中的伪类 CSS 伪类用于向某些选择器添加特殊的效果. 语法: selector : pseudo-class {property: value} CSS 类也可与伪类搭配使用 select ...
- CSS_Spirte实现原理 分类: HTML+CSS 2015-04-28 22:58 531人阅读 评论(0) 收藏
CSS Spirte就是所谓的把很多的小图标合并成一张大的图片,然后使用CSS的background-position属性,来动态的定位自己需要图标的位置.这样做的目的主要是减少HTTP请求,加快网页 ...
随机推荐
- java jar
http://www.cnblogs.com/shirui/p/5270969.html Java之 将程序打包成jar包 准备材料: 1.java文件: Helloworld.java pack ...
- App Store--心酸的上线路,说说那些不可思议的被拒理由
yoyeayoyea 您的应用包括色情内容(色情交易,色情展示). 原因是我们的销售人员,把几张艺术照放在个人相册里(头像),换成卡通头像,通过. 颜小风 被拒很正常 一次通过不正常. 之前上线 ...
- Swift 实现iOS Animation动画教程
这是一篇翻译文章.原文出处:http://www.raywenderlich.com/95910/uiview-animation-swift-tutorial 动画( animation)是iOS用 ...
- 百度云加速时使用Cloudflare的技术
百度云加速时使用Cloudflare的技术 引用“百度的关于我们”这是在打脸吗?就是把英文翻译过来换个验证码 百度是全球最大的中文搜索引擎.最大的中文网站.2000年1月创立于北京中关村.如今,百度已 ...
- myEclipse下安装SVN插件
step1.首先下载svn插件, step2.将下载下来的插件解压缩任意目录,找到里面的features 和plugins两个文件夹, step3.在myEclipse的安装目录下找到dropins文 ...
- HackRF实现无线门铃信号分析重放
文章特点:数据解码方面实在是没什么信心,存在分析错乱的可能性,所幸发出来共同探讨,恳请鞭策. 0x01 概述 这是一款工作在315Mhz频段的无线遥控门铃,根据查阅官方手册以及芯片信息,确定其采用了e ...
- Java中接口作为方法的返回
在<算法>中的散列表一节,在用拉链法实现散列表的API时要求实现以下一个方法: public Iterable<Key> keys() 我们知道Iterable是一个接口,那么 ...
- Git ~ 大杀器之一 远程仓库 ~ Git
一般情况ixashi找一台电脑作为服务器的角色 , 每天24小时开机 , 其他扥每个人都从这个 “服务器” 仓库里面克隆一份到自己的电脑上面 并且将各自的提交推送到服务器仓库中 , 也可以从服务器仓库 ...
- PHP中的数组(二)常用数组处理函数
数组的相关处理函数 一.数组键/值操作有关的函数 1.array_values() 无论是关联的还是索引的返回的都是索引数组 <?php $lamp=array(&quo ...
- Java 集合深入理解(13):Stack 栈
点击查看 Java 集合框架深入理解 系列, - ( ゜- ゜)つロ 乾杯~ 今天心情不错,再来一篇 Stack ! 数据结构中的 栈 数据结构中,栈是一种线性数据结构,遵从 LIFO(后进先出)的操 ...
