【hdu3341-Lost's revenge】DP压缩+AC自动机

题意：给定只含有A、G、C、T的n个模板串，一个文本串，文本串任意两个字母可互换位置，问最多能匹配多少个模板串。
注意：匹配同一个模板串匹配了两次，ans+=2；（可重复）

题解：

原本想到一个简单dp ： 开一个数组d[t1][t2][t3][t4][x]，t1~t4分别表示4个字母各有多少个，x表示当前位置。

然后这个数组为40*40*40*40*600，各种爆空间。

后来才知道要用压缩。。。

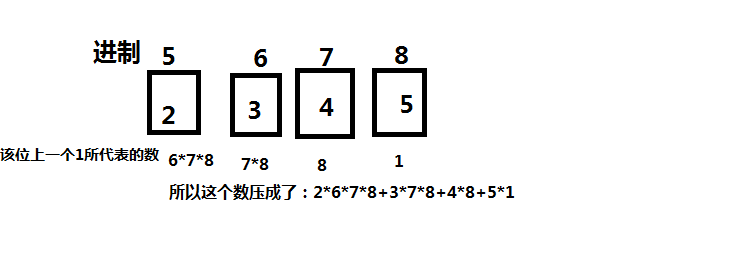
比如ACGT分别有5，6，7，8个。那t1为6进制，可以放0~5，t2为7进制……

然后类比10进制，把它压成一个10进制的数，这个数最大是11*11*11*11=14641.

压缩的原理：

我打了两个程序，dp一个用了递归，一个用了for循环，递归那个一直超时，for那个就A了。递归跟for循环差别这么大吗？

 //DP为for循环递推形式 AC
 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 #include<queue>
 using namespace std;

 const int N=;
 struct node{
     int sum,fail,son[];
 }a[N];
 queue<int> q;
 char s[N];
 int n,num,t[],sum[],k[],d[][N];
 bool vis[][N];
 int maxx(int x,int y){return x>y ? x:y;}
 int minn(int x,int y){return x<y ? x:y;}

 int idx(char c)
 {
     if(c=='A') return ;
     if(c=='G') return ;
     if(c=='C') return ;
     if(c=='T') return ;
 }

 void clear(int x)
 {
     a[x].fail=a[x].sum=;
     memset(a[x].son,,sizeof(a[x].son));
 }

 void trie(char *c)
 {
     int x=,l=strlen(c);
     for(int i=;i<l;i++)
     {
         int ind=idx(c[i]);
         if(!a[x].son[ind])
         {
             num++;
             clear(num);
             a[x].son[ind]=num;
         }
         x=a[x].son[ind];
     }
     a[x].sum++;
 }

 void buildAC()
 {
     while(!q.empty()) q.pop();
     for(int i=;i<=;i++)
         if(a[].son[i]) q.push(a[].son[i]);
     while(!q.empty())
     {
         int x=q.front();q.pop();
         int fail=a[x].fail;
         for(int i=;i<=;i++)
         {
             if(a[x].son[i])
             {
                 int y=a[x].son[i],z=a[fail].son[i];
                 a[y].fail=z;
                 a[y].sum+=a[z].sum;
                 q.push(a[x].son[i]);
             }
             else a[x].son[i]=a[fail].son[i];
         }
     }
 }

 int makeup()
 {
     return t[]*k[]+t[]*k[]+t[]*k[]+t[]*k[];
 }

 int dp()
 {
     memset(d,-,sizeof(d));
     d[][]=;
     int ans=,ss=sum[]+sum[]+sum[]+sum[];
     for(int l=;l<=ss;l++)//当前选择了多少个点
         for(int i=;i<=num;i++)//当前走到了第i个点
             for(t[]=maxx(,l-sum[]-sum[]-sum[]);t[]<=minn(l,sum[]);t[]++)//限制 最少选多少 最多选多少
                 for(t[]=maxx(,l-t[]-sum[]-sum[]);t[]<=minn(l,sum[]);t[]++)
                     for(t[]=maxx(,l-t[]-t[]-sum[]);t[]<=minn(l,sum[]);t[]++)
                     {
                         t[]=l-t[]-t[]-t[];
                         int now=makeup();
                         if(d[now][i]==-) continue;
                         ans=maxx(ans,d[now][i]);
                         for(int j=;j<=;j++)
                         {
                             int y=a[i].son[j];
                             if(t[j]+<=sum[j])
                             {
                                 t[j]++;
                                 int next=makeup();
                                 d[next][y]=maxx(d[next][y],d[now][i]+a[y].sum);
                                 t[j]--;
                             }
                         }
                     }
     return ans;
 }

 int main()
 {
     freopen("a.in","r",stdin);
     freopen("a.out","w",stdout);
     int T=;
     while()
     {
         scanf("%d",&n);
         if(!n) return ;
         num=;
         clear();
         for(int i=;i<=n;i++)
         {
             scanf("%s",s);
             trie(s);
         }
         buildAC();
         scanf("%s",s);
         int mx=,l=strlen(s);
         memset(sum,,sizeof(sum));
         memset(vis,,sizeof(vis));
         for(int i=;i<l;i++) sum[idx(s[i])]++;
         for(int i=;i<=;i++)
         {
             k[i]=;
             for(int j=i+;j<=;j++)
                 k[i]*=(sum[j]+);
             mx+=k[i]*sum[i];
         }
         printf("Case %d: %d\n",++T,dp());
     }
     return ;
 }

 //DP为递归形式 TLE
 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 #include<queue>
 using namespace std;

 const int N=;
 struct node{
     int sum,fail,son[];
 }a[N];
 queue<int> q;
 char s[N];
 int n,num,t[],sum[],k[],d[][N];
 bool vis[][N];
 int maxx(int x,int y){return x>y ? x:y;}
 int minn(int x,int y){return x<y ? x:y;}

 int idx(char c)
 {
     if(c=='A') return ;
     if(c=='G') return ;
     if(c=='C') return ;
     if(c=='T') return ;
 }

 void clear(int x)
 {
     a[x].fail=a[x].sum=;
     memset(a[x].son,,sizeof(a[x].son));
 }

 void trie(char *c)
 {
     int x=,l=strlen(c);
     for(int i=;i<l;i++)
     {
         int ind=idx(c[i]);
         if(!a[x].son[ind])
         {
             num++;
             clear(num);
             a[x].son[ind]=num;
         }
         x=a[x].son[ind];
     }
     a[x].sum++;
 }

 void buildAC()
 {
     while(!q.empty()) q.pop();
     for(int i=;i<=;i++)
         if(a[].son[i]) q.push(a[].son[i]);
     while(!q.empty())
     {
         int x=q.front();q.pop();
         int fail=a[x].fail;
         for(int i=;i<=;i++)
         {
             if(a[x].son[i])
             {
                 int y=a[x].son[i],z=a[fail].son[i];
                 a[y].fail=z;
                 a[y].sum+=a[z].sum;
                 q.push(a[x].son[i]);
             }
             else a[x].son[i]=a[fail].son[i];
         }
     }
 }

 int makeup(int t1,int t2,int t3,int t4)
 {
     return t1*k[]+t2*k[]+t3*k[]+t4*k[];
 }

 int dp(int now,int x)
 {
     int ans=,t1,t2,t3,t4;
     if(vis[now][x]) return d[now][x];
     t4=now%k[];
     t3=((now%k[])-(t4*k[]))/k[];
     t2=((now%k[])-(t4*k[]+t3*k[]))/k[];
     t1=(now-(t4*k[]+t3*k[]+t2*k[]))/k[];
     for(int i=;i<=;i++)
     {
         int y=a[x].son[i];
         if(!y && x) ans=maxx(ans,dp(now,));
         else if(i== && t1>=) ans=maxx(ans,a[y].sum+dp(makeup(t1-,t2,t3,t4),y));
         else if(i== && t2>=) ans=maxx(ans,a[y].sum+dp(makeup(t1,t2-,t3,t4),y));
         else if(i== && t3>=) ans=maxx(ans,a[y].sum+dp(makeup(t1,t2,t3-,t4),y));
         else if(i== && t4>=) ans=maxx(ans,a[y].sum+dp(makeup(t1,t2,t3,t4-),y));
     }
     d[now][x]=maxx(d[now][x],ans);
     vis[now][x]=;
     return d[now][x];
 }

 int main()
 {
     freopen("a.in","r",stdin);
     freopen("a.out","w",stdout);
     int T=;
     while()
     {
         scanf("%d",&n);
         if(!n) return ;
         num=;
         clear();
         for(int i=;i<=n;i++)
         {
             scanf("%s",s);
             trie(s);
         }
         buildAC();
         scanf("%s",s);
         int mx=,l=strlen(s);
         memset(sum,,sizeof(sum));
         memset(vis,,sizeof(vis));
         for(int i=;i<l;i++) sum[idx(s[i])]++;
         for(int i=;i<=;i++)
         {
             k[i]=;
             for(int j=i+;j<=;j++)
                 k[i]*=(sum[j]+);
             mx+=k[i]*sum[i];
         }
         // printf("%d\n",dp());
         memset(d,,sizeof(d));
         printf("Case %d: %d\n",++T,dp(mx,));
     }
     return ;
 }