9、改善深度神经网络之正则化、Dropout正则化

首先我们理解一下，什么叫做正则化？

　　目的角度：防止过拟合

　　简单来说，正则化是一种为了减小测试误差的行为(有时候会增加训练误差)。我们在构造机器学习模型时，最终目的是让模型在面对新数据的时候，可以有很好的表现。当你用比较复杂的模型比如神经网络，去拟合数据时，很容易出现过拟合现象(训练集表现很好，测试集表现较差)，这会导致模型的泛化能力下降，这时候，我们就需要使用正则化，降低模型的复杂度。

一、神经网路得L1、L2正则化

1、矩阵的F-1范数、F-2范数

说明：这里的F-范数指的是Frobenius范数，和logistics回归的L1、L2正则化的向量范数不一样。

矩阵的F-1范数：矩阵所有元素的绝对值之和。公式为：

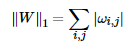
矩阵的F-2范数：矩阵所有元素的平方求和后开根号。公式为：

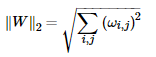
2、L1正则化与L2正则化（主要使用L2）

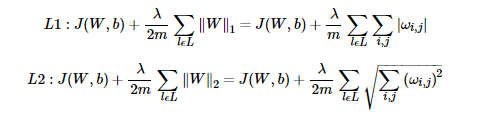
假设神经网络的损失函数为J(W,b)，参考逻辑回归的正则化，是在损失函数J(W,b)后面加一个正则化项，神经网络DNN也是一样的，只是变成了加F-范数，L1正则化与L2正则化如下所示：

这里m为样本数，l为各个隐藏层，λλ为超参数，需要自己调试，L2中2m是为了后面求梯度的时候可以抵消掉常数2。

3、L1正则化与L2正则化的区别

　　L1 正则化项的效果是让权值 W 往 0 靠，使网络中的权值尽可能为 0，也就相当于减小了网络复杂度，防止过拟合。事实上，L1 正则化能产生稀疏性，导致 W 中许多项变成零。

　　L2 正则化项的效果是减小权值 W。事实上，更小的权值 W，从某种意义上说，表示网络的复杂度更低，对数据的拟合刚刚好。

二、Dropout正则化（随机失活）

　　Dropout提供了正则化一大类模型的方法，计算方便且功能强大。它不同于L1、L2正则项那样改变损失函数。而是改变模型本身。Dropout可以被认为是集成大量深层神经网络的使用Bagging的方法。Dropout提供一种廉价的Bagging集成近似，能够训练和评估指数级数量的神经网络。

　　假设训练的网络：

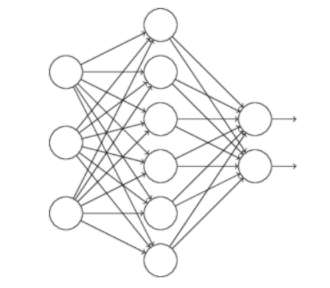
　　对于使用dropout技术的话，我们随机删除隐层的神经元，形成新的网络：

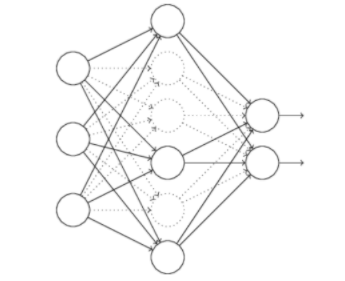
　　然后，我们通过前向求损失，反向传到损失，批量梯度下降完成一批，更新完w和b，然后继续随机删除隐藏层的神经元，继续批量梯度下降更新权值和偏置。

反向随机失活（inverted dropout）：

　　反向随机失活（inverted dropout），是在训练时就进行数值范围调整，从而让前向传播在测试时保持不变。这样做还有一个好处，无论你决定是否使用随机失活，预测方法的代码可以保持不变。

　　反向随机失活的代码如下：

"""

反向随机失活推荐实现方式

在训练时drop和调整数值范围，测试时不做任何事

"""

p = 0.5 #激活神经元得概率，P值更高=随机失活更弱

def train_step(x):

    #三层neural network的向前传播

    H1 = np.maximum(0,np.dot(w1,X) + b1)

    U1 = (np.random.rand(*H1.shape) < p) / p #第一个随机失活遮罩。注意P！！！

    H1 *=U1 #drop!

    H2 = np.maximum(0,np.dot(w2,H1) + b2)

    U2 = (np.random.rand(*H2.shape) < p) / p #第一个随机失活遮罩。注意P！！！

    H2 *=U2 #drop!

    out = np.dot(w3,H2)+b3

    #反向传播：计算梯度。。。（略）

    #进行参数更新。。。（略）

def predict(X):

    # 向前传播时模型集成

    H1 = np.maximum(0,np.dot(w1,X) + b1) #不用进行数值范围调整

    H2 = np.maximum(0,np.dot(w2,H1) + b2)

    out = np.dot(w3,H2) + b3