Table.Combine追加…Combine（Power Query 之 M 语言）

数据源：

销量表和部门表

目标：

其中一表的数据追加到另一表后面，相同列直接追加，不同列增加新列

操作过程：

选取销量表》【主页】》【追加查询】/【将查询追加为新查询】》选择要追加的表》【确定】

　　

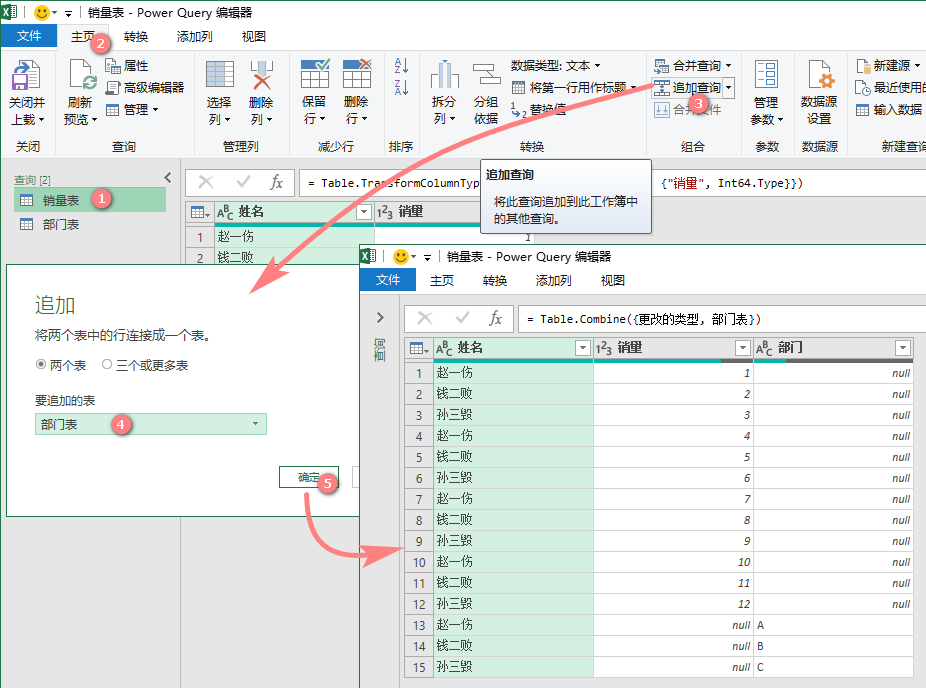
M公式：

　　 = Table.Combine({表1,表2,...,表n}, {"追加列1",...,"追加列n"})

最终效果：

如图

扩展：

　　列表追加：= List.Combine({列表1,列表2,...,列表n})

　　记录追加：= Record.Combine({记录1,记录2,...,记录n})

　　任意追加：&

　　　　= 表1 & 表2 &...& 表n 

　　　　= 列表1 & 列表2 &...& 列表n

　　　　= 记录1 & 记录2 &...& 记录n

　　合并…Combine…