【Lucas组合数定理】组合-FZU 2020

组合 FZU-2020

题目描述

给出组合数C(n,m), 表示从n个元素中选出m个元素的方案数。例如C(5,2) = 10, C(4,2) = 6.可是当n,m比较大的时候，C(n,m)很大！于是xiaobo希望你输出 C(n,m) mod p的值！

分析

Lucas定理：

如果我们要求C(n,m)%p的值，那么

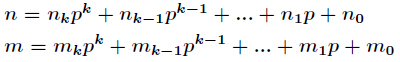
进行推导可以得到

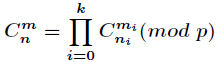
这一道题使用Lucas定理的递归式

\[C^n_m \ mod \ p= C^{n\ mod \ p}_{m\ mod \ p}\times C^{n\div p}_{m\div p} \ mod \ p
\]

Lucas递归边界，\(m=0\) 那么值就是1，其余部分递归处理，

剩下的$ C(n%mod,m%mod) $就可以使用费马小定理或者扩展欧几里得来求出逆元算一下答案就可以了。

AC代码

#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <cctype>
#include <cmath>
#include <time.h>
#include <map>
#include <set>
#include <vector>
using namespace std;
#define ms(a,b) memset(a,b,sizeof(a))
typedef long long ll;
ll n,m,p;
inline int read(){
    int X=0,w=0; char ch=0;
    while(!isdigit(ch)) {w|=ch=='-';ch=getchar();}
    while(isdigit(ch)) X=(X<<3)+(X<<1)+(ch^48),ch=getchar();
    return w?-X:X;
}
ll power(ll a,ll b) {
	ll res=1;
	while(b>0) {
		if (b&1) res=res*a%p;
		b=b>>1;
		a=a*a%p;
	}
	return res;
}
ll C(ll n,ll m) {
	if (m>n) return 0;
	ll ans=1;
	for (int i=1;i<=m;i++) {
		ll a=(n+i-m)%p;
		ll b=i%p;
		ans=ans*(a*power(b,p-2)%p)%p;
	}
	return ans;
}
ll lucas(ll n,ll m) {
	if (m==0) return 1;
	return C(n%p,m%p)*lucas(n/p,m/p)%p;
}
int main(){
	int cas=read();
	while (cas--) {
		scanf("%lld%lld%lld",&n,&m,&p);
		printf("%lld\n",lucas(n,m));
	}
	return 0;
}