Improved Variational Inference with Inverse Autoregressive Flow

目录

• 概
• 主要内容
• 代码

Kingma D., Salimans T., Jozefowicz R., Chen X., Sutskever I. and Welling M. Improved Variational Inference with Inverse Autoregressive Flow. NIPS, 2016.

概

一种较为复杂normalizing flow.

主要内容

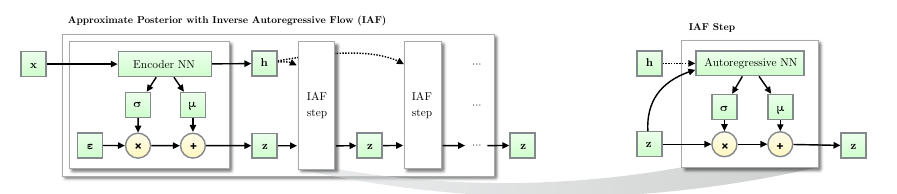
IAF的流程是这样的:

1. 由encoder 得到\(\mu, \sigma, h\), 采样\(\epsilon\), 则

\[z_0 = \mu_0 + \sigma_0 \odot \epsilon;
\]

1. 由自回归模型得到\(\mu_1, \sigma_1\), 则

\[z_1 = \mu_1 + \sigma_1 \odot z_{0};
\]

1. 依次类推:

\[z_t = \mu_t + \sigma_t \odot z_{t-1};
\]

自回归模型的特点就是:

\[\hat{v} = f(v), \quad f: \mathbb{R}^D \rightarrow \mathbb{R}^D, \\
\]

\(\nabla_v f\)是一个对角线元素为0的下三角矩阵.

我们来看\(\nabla_{z_{t-1}}z_{t}\),

\[\nabla z_t = \nabla \mu_t + \mathrm{diag}(z_{t-1}) \nabla \sigma_t + \mathrm{diag}(\sigma_t).
\]

显然, \(\nabla_{z_{t-1}} z_t\)也是一个下三角矩阵, 且

\[\mathrm{det} \nabla z_t = \mathrm{det} \: \mathrm{diag}(\sigma_t)= \prod_{i=1}^D (\sigma_t)_i.
\]

这个计算方式就相当简单了.

总结一下, 最后的

\[\log q(z_T|x) = -\sum_{i=1}^D( \frac{1}{2} \epsilon_i^2 + \frac{1}{2}\log (2\pi) + \sum_{t=0}^T \log \sigma_{t,i}).
\]

代码

原文代码

pytorch-version-kefirski

pytorch-version-pclucas14