强化学习（五）—— 策略梯度及reinforce算法

1 概述

　　在该系列上一篇中介绍的基于价值的深度强化学习方法有它自身的缺点，主要有以下三点：

　　1）基于价值的强化学习无法很好的处理连续空间的动作问题，或者时高维度的离散动作空间，因为通过价值更新策略时是需要对每个动作下的价值函数的大小进行比较的，因此在高维或连续的动作空间下是很难处理的。

　　2）在基于价值的强化学习中我们用特征来描述状态空间中的某一状态时，有可能因为个体观测的限制或者建模的局限，导致真实环境下本来不同的两个状态却再我们建模后拥有相同的特征描述，进而很有可能导致我们的value Based方法无法得到最优解。如下图：

　　　　

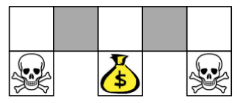
　　　　当有些个体选择比较容易观测的特征来描述状态空间时，比如颜色，则在上图中两个灰色格子（代表着两个不同的状态）的特征表示是一样的，倘若我们的最终目的是要获得金币，则当你在左边的灰色格子时，你需要往右移；当你在右边的灰色格子时，你需要往左移。而在基于价值的强化学习方法中，策略往往时确定的，也就是你的状态确定了，动作就确定了，那么在这里如果两个灰色格子的状态是一样，则执行的动作是一样的。这显然是不行的。

　　3）无法解决随机策略问题，基于价值的强化学习的策略是确定的（当然也可以用$\epsilon-greedy$，但是随机性没那么强），而基于策略的强化学习是具有随机性的。

2 策略梯度

　　首先来从似然率的角度推到策略梯度：

　　给定一组状态-动作序列$\tau = s_0, a_0, s_1, a_1, ......, s_l, a_l。

　　则有$R(\tau) = \sum_{t=0}^l R(s_t, a_t)$表示序列$\tau$的回报。$P(\tau; \theta)$表示序列$\tau$出现的概率，则策略梯度的目标函数可以表示为：

　　　　$J(\theta) = E(\sum_{t=0}^l R(s_t, a_t); \pi_{\theta}) = \sum_{\tau} P(\tau; \theta)R(\tau)$

　　策略梯度的目标就是找到最优参数$\theta$，使得$J(\theta)$最大。因此策略梯度是一个优化问题，最简单的就是用梯度上升法来求解：

　　　　$\theta = \theta + \alpha \nabla_{\theta}J(\theta)$

　　现在我们来对目标函数求导：

　　　　$ \nabla_{\theta}J(\theta) =  \nabla_{\theta}\sum_{\tau} P(\tau; \theta)R(\tau)$

　　　　$=\sum_{\tau} \nabla_{\theta}P(\tau; \theta)R(\tau)$

　　　　$=\sum_{\tau} \frac{P(\tau; \theta)}{P(\tau; \theta)} \nabla_{\theta}P(\tau; \theta)R(\tau)$

　　　　$=\sum_{\tau} P(\tau; \theta)\frac{\nabla_{\theta}P(\tau; \theta)R(\tau)}{P(\tau; \theta)}$

　　　　$=\sum_{\tau} P(\tau; \theta) \nabla_{\theta} \log{P(\tau; \theta)}R(\tau)$

　　因此最终的策略梯度就变成求$ \nabla_{\theta} \log{P(\tau; \theta)}R(\tau)$的期望了，这样当采样$m$条样本序列时，就可以利用$m$条序列的均值逼近策略梯度的期望：

　　　　$ \nabla_{\theta}J(\theta) = \frac{1}{m} \sum_{i=1}^m \nabla_{\theta} \log{P(\tau; \theta)}R(\tau)$

　　从上面的式子可以看出第一项$\nabla_{\theta} \log{P(\tau; \theta)}$是轨迹$\tau$ 的概率随参数$\theta$变化最陡的方向。第二项$R(\tau)$控制了参数更新的方向和步长。

　　对于每一条序列$\tau$的概率$P(\tau; \theta)$都可以表示成下面的形式：

　　　　$P(\tau^i; \theta) = \prod_{t=0}^l P(s_{t+1}^i | s_t^i, a_t^i) \pi_{\theta}(a_t^i | s_t^i)$

　　对上面的式子代入到梯度的式子中，通过对数展开可以得到：

　　　　$ \nabla_{\theta}J(\theta) = \frac{1}{m} \sum_{i=1}^m (\sum_{t=0}^l \nabla_{\theta} \log{\pi_{\theta} (a_t^i | s_t^i)}R(\tau^i))$

　　但是上面的式子有一个问题，就是后面的$R(\tau^i)$是对整条序列的回报，但是在$t$时刻的策略对应的回报不应该和$t$时刻之前的状态-动作价值无关。因此对这个式子进行修改可以得到：

　　　　$\nabla_{\theta} J(\theta) = \mathbb{E}_{\pi_{\theta}}[\nabla_{\theta}log \pi_{\theta}(s,a) Q_{\pi}(s,a)]$

　　在上面的式子中$\nabla_{\theta}log \pi_{\theta}(s,a)$ 是不会改变的，这个一般称为分值函数，但后面的$Q_{\pi}(s,a)$是可能发生改变的。

　　除了这个问题之外，还有一个问题就是策略梯度$\nabla_{\theta}J(\theta)$的方差很大，这个时候一般引入一个常数基线b，即：

　　　　$\nabla_{\theta} J(\theta) = \mathbb{E}_{\pi_{\theta}}[\nabla_{\theta}log \pi_{\theta}(s,a) (Q_{\pi}(s,a) - b)]$

　　这个常数的引入不会影响到梯度的值（证明忽略），但是在某一个b值下可以使得梯度的方差最小。

3 策略函数

　　我们上面抽象的用一个函数表示了策略函数，那策略函数的具体形式是什么样子的呢？一般来说，对于离散的动作空间，用softmax函数来描述；对于连续的动作空间，用高斯函数来描述。

　　在离散的动作空间中，softmax函数描述了各个动作被选中的概率，在构建网络时可以当作是一个多分类的问题：

　　　　$\pi_{\theta}(s,a) = \frac{e^{\phi(s,a)^T\theta}}{\sum\limits_be^{\phi(s,b)^T\theta}}$

　　其中$\phi(s,a)$表示的是给定状态s，动作a的特征表示。

　　在连续的动作空间中，策略产生动作是遵循高斯分布$\mathbb{N(\phi(s)^T\theta, \sigma^2)}%$的。

4 reinforce算法流程

　　在蒙特卡洛策略梯度reinforce算法，我们用价值函数$v(s)$近似的替代上面的目标函数中的$Q(s, a)$。则整个流程如下：

　　假设迭代轮数为EPISODES，采样的序列最大长度为L，学习速率为$\alpha$，状态集为S，动作集为A。

　　1）for episode in range(EPISODES):   # 开始迭代

　　2）初始化状态s，在这里s为状态向量

　　3）for step in range(T):  # 序列采样

　　　　a) 将状态向量s输入到策略函数中，我们可以得到softmax之后每个动作的概率，根据概率去选择动作（增加了随机性，而不是每次选择概率最大的动作）；

　　　　b) 在状态s下执行当前动作$a$，获得下一状态$s‘$，当前奖励$R$，是否终止状态${is\_end}$；

　　　　c) 将当前的状态$s$，动作$a$，奖励$R$分别存储在一个列表中；

　　　　d) 更新状态，$s = s'$；

　　　　e) 判断是否是最终状态，如果是则将这条采样得到的序列用来更新策略函数中的参数；否则继续循环采样。