求小于n的素数个数

本文是对 LeetCode Count Primes 解法的探讨。

题目：

Count the number of prime numbers less than a non-negative number, n.

尽管题目并没有要我们写一个最优的算法，但是身为一个程序员，优化应该是一种习惯，在编程的过程中，随着思考进行优化。只要求我们满足给定的时间和空间即可。

如果你只能想出一个最简单的方法，难道你会有什么竞争力吗？

穷举

最开始我用的就是这个方法，可以说这是最简单的一种方法了，而且最开始，我就是想的这种方法，说明：我没有对这个问题进行思考，没有去优化它，而作为一个程序员，如何提高效率是拿到一个问题首先要思考的事情。

public int countPrimes(int n) {
    int num = 0;
    for (int i = 2; i < n; i++) {
        boolean flag = true;
        for (int j = 2; j < i - 1; j++)
            if (i % j == 0) {
                flag = false;
                break;
            }
        if (flag) {
            num++;
        }
    }
    return num;
}

测试代码：

public static void main(String[] args) {
    //获取开始时
    long startTime = System.currentTimeMillis();
    System.out.println("The num is " + new L_204_Count_Primes().countPrimes(2000000));
    long endTime = System.currentTimeMillis();
    //获取结束时间
    System.out.println("程序运行时间： " + (endTime - startTime) + "ms");
}

时间太长，已经不能计算。

只能是奇数且小于\(\sqrt{n}\)

思考后发现

1. 素数一定是奇数
2. 若 n=ab 是个合数（其中 a 与 b ≠ 1）, 则其中一个约数 a 或 b 必定至大为 \(\sqrt{n}\).

public int countPrimes2(int n) {
    int num = 1;
    for (int i = 3; i < n; i += 2) {
        boolean flag = true;
        for (int j = 2; j <= (int) Math.sqrt(i); j++)
            if (i % j == 0) {
                flag = false;
                break;
            }
        if (flag) {
            num++;
        }
    }
    return num;
}

The num is 148933

程序运行时间： 1124ms

试除法：数学知识的运用

查阅 算术基本定理可知：

算术基本定理 :

每个大于1的整数均可写成一个以上的素数之乘积，且除了质约数的排序不同外是唯一的

也就是说我们可以每个数来除以得到的素数，这样可大大减少运行次数。

public int countPrimes3(int n) {
    if (n < 3) {
        return 0;
    }
    //0 1 不算做素数,2一定是素数
    List<Integer> list = new ArrayList<>();
    list.add(2);
    boolean flag;
    for (int i = 3; i < n; i += 2) {
        flag = true;
        for (int j = 0; j < list.size() && list.get(j) <= (int) Math.sqrt(n); j++) {
            if (i % list.get(j) == 0) {
                flag = false;
                break;
            }
        }
        if (flag) {
            list.add(i);
        }
    }
    return list.size();
}

The num is 148933

程序运行时间： 383ms

筛选法

埃拉托斯特尼筛法，简称埃氏筛，也有人称素数筛。这是一种简单且历史悠久的筛法，用来找出一定范围内所有的素数。

所使用的原理是从2开始，将每个素数的各个倍数，标记成合数。一个素数的各个倍数，是一个差为此素数本身的等差数列。此为这个筛法和试除法不同的关键之处，后者是以素数来测试每个待测数能否被整除。

筛选法的策略是将素数的倍数全部筛掉，剩下的就是素数了，下图很生动的体现了筛选的过程：

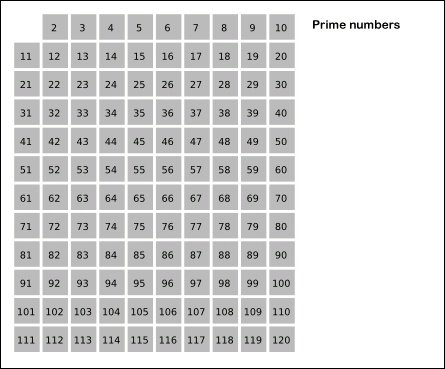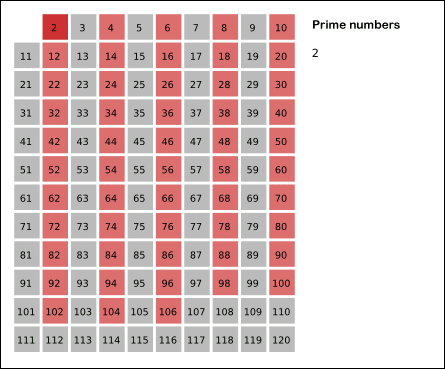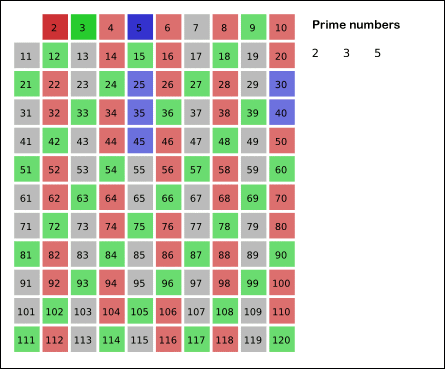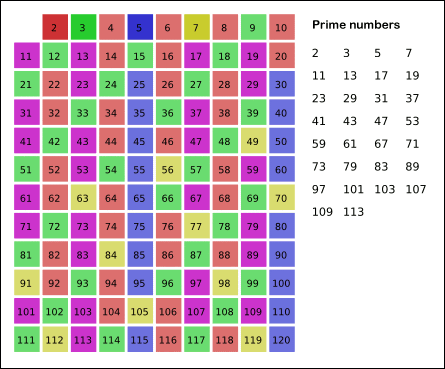
筛选的过程是先筛掉非素数，针对本文的题目，每筛掉一个，素数数量-1即可，上面说过素数的一个特点，除了2，其它的素数都是奇数，所以我们只需在奇数范围内筛选就可以了。

public int countPrimes4(int n) {
    if (n < 3) {
        return 0;
    }
    //false代表素数，true代表非素数
    boolean[] flags = new boolean[n];
    //0不是素数
    flags[0] = true;
    //1不是素数
    flags[1] = true;
    int num = n - 2;
    for (int i = 2; i <= (int) Math.sqrt(n); i++) {
        //当i为素数时，i的所有倍数都不是素数
        if (!flags[i]) {
            for (int j = 2 * i; j < n; j += i) {
                if (!flags[j]) {
                    flags[j] = true;
                    num--;
                }
            }

        }
    }
    return num;
}

The num is 148933

程序运行时间： 43ms

全部代码放在：

https://github.com/morethink/algorithm/blob/master/src/algorithm/leetcode/L_204_Count_Primes.java

参考文档：

1. 求质数算法的N种境界[1] - 试除法和初级筛法
2. 求素数个数
3. 埃拉托斯特尼筛法