【codevs 1911 孤岛营救问题】

·为了分析方便，可以先做一个题目简化。去掉“钥匙”这个条件，那么就是一个BFS或者SPFA……现在加上该条件。如本题只给出最多两种钥匙，当然你可以继续坚持BFS等方式，时间不会太差。但是一旦钥匙种类上升至15的时候，就有太多情况需要处理(光说你写BFS的if就是很长的过程，但个人认为时间复杂度依旧能过这道题)。

·如图是简化版本的决策方式(为与后文呼应,用SPFA)：

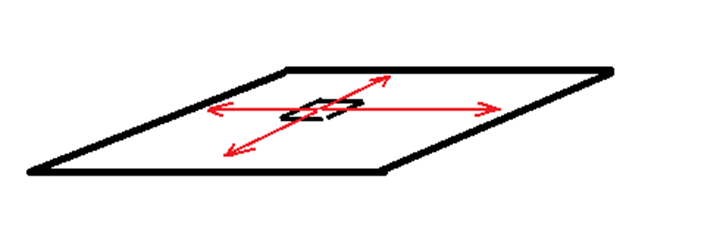
大方块是整个地图。小方块是一个房间。那么你可以在向四个方向走，前提是有路可走(没有墙)。你本可以轻松拯救大兵瑞恩，然后过上幸福快乐的生活，但是你可能在实际问题中遭遇这样的绝望情况：

       明明有路可走，但是那扇门你没有钥匙。现在你开始幻想，怎样才能走过去呢……你妄想：要是在这之前有开这扇门的钥匙就好了，那我同样是走相同的路来到这扇门前，但是在那个时空的我就可以轻松开门，这个时空的我就只能绝望地去他地寻找钥匙。

·我们谈到了时空断裂。那么就干脆把每个时空也作为状态的一部分吧！（注意，在这之前你的状态只有一个元素，就是当前点坐标）。

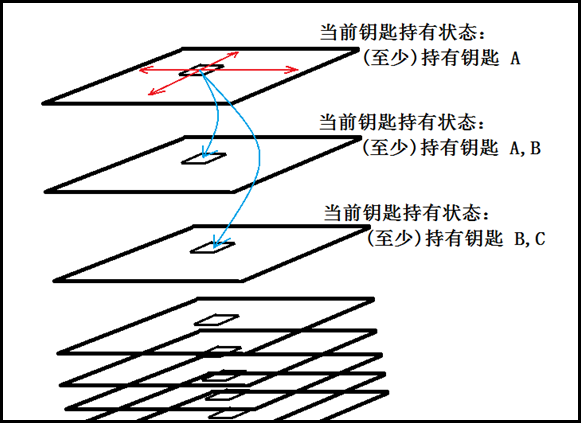
·由图可见，你要时空穿梭的条件是你必须具备相应的钥匙。图中：如果你在这个房间里捡到了B,C钥匙，那么就有这种穿越方式(蓝色有向边)。由于在这里“时空”与“坐标位置”的地位是相同的【它们无制约关系】。也就是说你穿越两次时空在向左走一步，和将这些动作反过来，在可行的情况下是等价的。说明这一点的目的在于：这启示我们,其实这图中6条边的意义是相同的。

         这样一来，这道题就变成了普通的最短路问题，只是路多了些，判断条件多了些。所以可以用二维状态来表示当前情况，最终答案在每个时空里找一个最优的即可(没喊你把所有钥匙拿完啊！)。

 1 #include<bits/stdc++.h>
 2 #define go(i,a,b) for(int i=a;i<=b;i++)
 3 #define fo(i,a,x) for(int i=a[x];i>-1;i=e[i].next)
 4 #define mem(a,b) memset(a,b,sizeof(a))
 5 #define P 3000
 6 #define inf 0x3f3f3f3f
 7 using namespace std;const int N=203;
 8 int dx[4]={0,0,1,-1},dy[4]={1,-1,0,0};
 9 int n,m,p,f,S[N][N],id[N][N],key[N],head[N],k=0,s,t,dis[P][N];
10 struct E{int v,next,rar;}e[N*N*4];bool inq[P][N];
11 void ADD(int u,int v,int rar){e[k]=(E){v,head[u],rar};head[u]=k++;}
12 struct G{int x,y;};
13 int spfa()
14 {
15     mem(dis,0x3f);dis[1][1]=0;inq[1][1]=1;
16     queue<G>q;q.push((G){1,1});
17     while(!q.empty())
18     {
19         G U=q.front();q.pop();inq[U.x][U.y]=0;
20         dis[U.x|key[U.y]][U.y]=min(dis[U.x|key[U.y]][U.y],dis[U.x][U.y]);
21         U.x|=key[U.y];
22
23         fo(i,head,U.y)if(U.x%(e[i].rar<<1)>=e[i].rar)
24         {
25             int v=e[i].v;
26             if(dis[U.x][v]>dis[U.x][U.y]+1)
27             {
28                 dis[U.x][v]=dis[U.x][U.y]+1;
29                 if(!inq[U.x][v])
30                 {
31                     inq[U.x][v]=1;
32                     q.push((G){U.x,v});
33                 }
34             }
35         }
36     }
37     int ret=inf;go(i,1,P-1)ret=min(ret,dis[i][t]);
38     if(ret==inf)ret=-1;return ret;
39 }
40
41 int main()
42 {
43
44     int k,a,b,c;mem(S,-1);mem(head,-1);
45     scanf("%d%d%d%d",&n,&m,&p,&f);
46     go(i,1,n)go(j,1,m)id[i][j]=++t;
47     go(i,1,f){scanf("%d%d",&a,&b);a=id[a][b];
48         scanf("%d%d",&b,&c);b=id[b][c];
49         scanf("%d",&c);S[a][b]=S[b][a]=c;
50         if(c)ADD(a,b,1<<c),ADD(b,a,1<<c);}
51
52     go(i,1,n)go(j,1,m)
53     {
54         a=id[i][j];go(k,0,3)
55         {
56             int x=i+dx[k],y=j+dy[k];b=id[x][y];
57             if(S[a][b]==-1&&b)ADD(a,b,1);
58         }
59     }
60     scanf("%d",&f);
61     go(i,1,f)scanf("%d%d%d",&a,&b,&c),key[id[a][b]]|=(1<<c);
62     printf("%d\n",spfa());
63     return 0;
64 }

【大米饼代码】

·最后来一句关于代码疑难的提示：

到达同一个地点时，手上的钥匙越多越好，不要害怕。

比起那些政客的谎言，我们要圣洁得多。