Luogu P1314 聪明的质监员(二分+前缀和)

P1314 聪明的质监员

题意

题目描述

小\(T\)是一名质量监督员，最近负责检验一批矿产的质量。这批矿产共有\(n\)个矿石，从\(1\)到\(n\)逐一编号，每个矿石都有自己的重量\(w_i\)以及价值\(v_i\)。检验矿产的流程是：

1. 给定\(m\)个区间\([L_i,R_i]\)

2. 选出一个参数\(W\)；

3. 对于一个区间\([L_i,R_i]\)，计算矿石在这个区间上的检验值\(Y_i\)

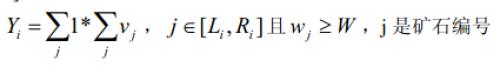
这批矿产的检验结果\(Y\)为各个区间的检验值之和。即：\(Y_1+Y_2...+Y_m\)

若这批矿产的检验结果与所给标准值\(S\)相差太多，就需要再去检验另一批矿产。小\(T\)不想费时间去检验另一批矿产，所以他想通过调整参数\(W\)的值，让检验结果尽可能的靠近标准值\(S\)，即使得\(S-Y\)的绝对值最小。请你帮忙求出这个最小值。

输入输出格式

输入格式：

第一行包含三个整数\(n,m,S\)，分别表示矿石的个数、区间的个数和标准值。

接下来的\(n\)行，每行\(2\)个整数，中间用空格隔开，第\(i+1\)行表示\(i\)号矿石的重量\(w_i\)和价值\(v_i\)。

接下来的\(m\)行，表示区间，每行\(2\)个整数，中间用空格隔开，第\(i+n+1\)行表示区间\([L_i,R_i]\)的两个端点\(L_i\)和\(R_i\)。注意：不同区间可能重合或相互重叠。

输出格式：

一个整数，表示所求的最小值。

输入输出样例

输入样例：

5 3 15
1 5
2 5
3 5
4 5
5 5
1 5
2 4
3 3

输出样例：

10

说明

【输入输出样例说明】

当\(W\)选\(4\)的时候，三个区间上检验值分别为\(20,5,0\)，这批矿产的检验结果为 \(25\)，此时与标准值\(S\)相差最小为\(10\)。

【数据范围】

对于\(10 \%\)的数据，有\(1 \leq n,m \leq 10\)；

对于\(30 \%\)的数据，有\(1 \leq n,m \leq 500\)；

对于\(50 \%\)的数据，有\(1 \leq n,m \leq 5,000\)；

对于\(70 \%\)的数据，有\(1 ≤n,m \leq 10,000\)；

对于\(100\%\)的数据，有\(1 \leq n,m \leq 200,000, \ 0<w_i,v_i≤10^6, \ 0<S \leq 10^{12},1 \leq L_i \leq R_i \leq n\)。

思路

我点错\(ans\)文件了。 --alecli

今天下午应alecli大佬之邀来刷\(NOIP\)的各种蓝题，然后就做到了这一道。

开头的那张公式图片看得我一脸懵逼，不过想一想也还是能像清楚的。一共有\(n\)个物品，每个物品有两个属性\(w\)和\(v\)。我们选取一个\(W\)，然后对于每一段区间，其中所有\(w\)属性大于\(W\)的物品的数量乘上这些物品的\(v\)值之和，就是这一段区间的\(Y\)值。把每个区间的\(Y\)值加起来，就是总\(Y\)值。题目要求的，就是总\(Y\)值与给定的数\(S\)的最小差值。

有两点显然的特性：

1. 选的\(W\)越大，每个区间所满足\(w\)属性大于\(W\)的物品的数量越大；
2. 选的\(W\)越大，这些物品的\(v\)值之和也越大。

因为\(Y\)与这两个属性正相关，所以\(Y\)关于\(W\)单调递增，那么我们就可以二分\(W\)的值，来计算\(Y\)了。

第二个问题就是如何快速地计算\(Y\)。因为对于没一段区间我们都只询问区间和，所以很容易想到预处理\(O(n)\)，查询\(O(1)\)的前缀和。具体来说我们这样操作：

tmp=0;//统计Y值
memset(s,0,sizeof s);//s是v的前缀和
memset(cnt,0,sizeof cnt);//cnt是数量的前缀和
for(LL i=1;i<=n;i++)//预处理
{
    if(w[i]>=W) s[i]=s[i-1]+v[i],cnt[i]=cnt[i-1]+1;//满足w>=W，对答案有贡献
    else s[i]=s[i-1],cnt[i]=cnt[i-1];//对答案无贡献
}
for(LL i=1;i<=m;i++) tmp+=(s[r[i]]-s[l[i]-1])*(cnt[r[i]]-cnt[l[i]-1]);//查询每一段区间的Y值

顺利\(AC\)。

AC代码

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL MAXN=2e5+5;
LL n,m,S,sum,tmp,ans=LLONG_MAX,L=LLONG_MAX,R=LLONG_MIN;
LL w[MAXN],v[MAXN],l[MAXN],r[MAXN],s[MAXN],cnt[MAXN];
LL read()
{
    LL re=0;
    char ch=getchar();
    while(!isdigit(ch)) ch=getchar();
    while(isdigit(ch)) re=(re<<3)+(re<<1)+ch-'0',ch=getchar();
    return re;
}
LL check(LL lzq)
{
    tmp=0;
    memset(s,0,sizeof s);
    memset(cnt,0,sizeof cnt);
    for(LL i=1;i<=n;i++)
    {
        if(w[i]>=lzq) s[i]=s[i-1]+v[i],cnt[i]=cnt[i-1]+1;
        else s[i]=s[i-1],cnt[i]=cnt[i-1];
    }
    for(LL i=1;i<=m;i++) tmp+=(s[r[i]]-s[l[i]-1])*(cnt[r[i]]-cnt[l[i]-1]);
    sum=tmp-S;
    if(sum<0) sum=-sum;
    return tmp>S;
}
int main()
{
    n=read(),m=read(),S=read();
    for(LL i=1;i<=n;i++) w[i]=read(),v[i]=read(),L=min(L,w[i]),R=max(R,w[i]);
    for(LL i=1;i<=m;i++) l[i]=read(),r[i]=read();
    while(L<=R)
    {
        LL mid=(L+R)>>1;
        if(!check(mid)) R=mid-1;
        else L=mid+1;
        if(ans>sum) ans=sum;
    }
    printf("%lld",ans);
    return 0;
}