用GM找到机器码

基址   400000

偏移是401940-400000 = 0x1940

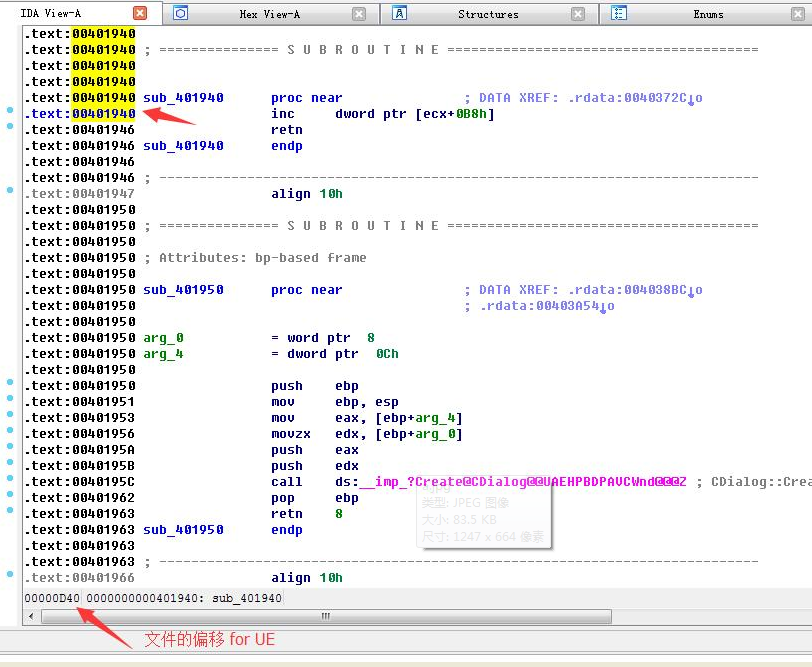
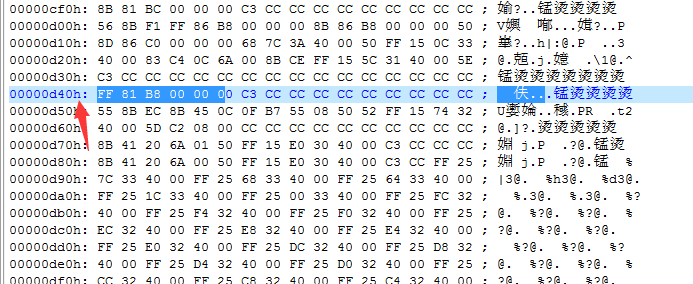
UE去到D40位置修改

IDA修改游戏的更多相关文章

  1. unity远程修改游戏配置

    关于修改游戏配置这点,如果pc还好 但是在移动端,比较麻烦,比如游戏换ip地址了,可能需要重新打包了 那能不能动态修改,这里有个思路 以udp举例 在客户端里面写一个udp服务,在游戏第一界面打开,比 ...

  2. 如何使用FlashgameMaster修改游戏

    1 打开任意一款游戏,注意最好是AS2.0版的,我们以黄金矿工为例. 2 使用方法: 点击编辑按钮的打开编辑面板出现编辑面板后在对话框中输入要查找的数值,点击查找按钮,会列表出所以等于该值的变量. 如 ...

  3. [IDA]修改变量类型、删除变量名

    1. 双击变量 2. 按D转换类型(Word.Byte.Dword) 3. 按U删除变量名 4. 按N修改变量名

  4. IDA 修改后保存

    关键点找到了.把 jz short loc_10004753 改成jnz short loc_10004753即可. IDA->edit->Patch program->Assemb ...

  5. Cocos2d-x单机游戏防八门神器修改数据

    来源:http://cocos2d.9tech.cn/news/2014/0212/39812.html 网上的cocos2d-x教程多为知识点的讲解,但我们学习cocos2d-x的目的是为了什么?为 ...

  6. 只需要一点点C++基础，新手也可以制作单机游戏内存修改器

    声明:本文只是为了初学C++的,能够做出一些实用的东西,跳出管理系统的束缚,提升学习的兴趣,在这里选取了单机游戏,请不要尝试在线游戏,违发而已未必可行.序:首先我们需要一个Qt+VS环境Qt从http ...

  7. IDA硬编码修改SO,重新打包APK绕过FRIDA反调试

    该案例来自看雪 通过IDA修改SO 找到检测点 修改字符串 双击该字符串进入TEXT VIEW 选择 HEX VIEW 修改十六进制 右击EDIT 修改字符 右击 菜单栏-> edit -> ...

  8. Lua游戏逆向及破解方法介绍

    Lua游戏逆向及破解方法介绍   背景介绍 随着手游的发展,越来越多的Cocos-lua端游开发者转移到手游平台.Lua脚本编写逻辑的手游也是越来越多,如梦幻西游.刀塔传奇.开心消消乐.游龙英雄.奇迹 ...

  9. Android逆向之旅---Android应用的汉化功能(修改SO中的字符串内容)

    一.前言 今天我们继续来讲述逆向的知识,今天我们来讲什么呢?我们在前一篇文章中介绍了关于SO文件的格式,今天我们继续这个话题来看看如何修改SO文件中的内容,看一下我们研究的主题: 需求:想汉化一个Ap ...

随机推荐

  1. poj 2524 求连通分量（并查集模板题）

    求连通分量 Sample Input 10 91 21 31 41 51 61 71 81 91 1010 42 34 54 85 80 0Sample Output Case 1: 1Case 2: ...

  2. 只想写一个真正能用的django mock

    调参数的过程,百转千回. 还好,搞得差不多了. 确实,方便写测试用例, 也是一个开发水平高低的衡量~~~:( 为了测试这个mock,不得不改下代码~~ 还要不断的将Model里允许Null的参数写完, ...

  3. 关于 win10 创建WiFi热点 问题（无法启动承载网络 ， 我们无法设置移动热点，因为你的电脑未建立以太网，wifi或手机网络数据连接 ）

    电脑创建WiFi,一般三种办法: 1. WiFi共享软件:猎豹wifi.wifi共享精灵.wifi共享大师..... 2. 命令提示符 netsh wlan set hostednetwork mod ...

  4. 002.etcd使用场景

    引用链接: https://blog.csdn.net/linuxheik/article/details/77853119 https://www.cnblogs.com/doscho/p/6221 ...

  5. 社会地位即服务, Status as a Service (一): 社交网络是一种 ICO 行为？

    上周,看到 Eugene Wei 又发了一篇长文,Status as a Service (StaaS).状态即服务?服务器的状态吗?不知所言.抱着好奇,我打开了这篇文章,一看就是 3 个小时!

  6. Android-LayoutAnimation

    Android-LayoutAnimation 学习自 <Android开发艺术探索> LayoutAnimation漫谈 LayoutAnimation 也是View动画的一种,作用是为 ...

  7. SQL语句之 数据约束

    SQL语句之 数据约束 什么是数据约束 数据约束用来限制用户对数据的非法的修改操作. 1.约束字段的默认值 如果插入记录时,没有给某个字段赋值,那么我们可以设置它的默认值 关键字:default CR ...

  8. react比较入门的小demo

    什么是jsx?    JSX是JavaScript  XML 这两个单词的缩写,xml和html非常类似,简单来说可以把它理解成使用各种各样的标签,大家可以自行 百度.所以jsx就是在javascri ...

  9. android 设置为系统应用

    韩梦飞沙  韩亚飞  313134555@qq.com  yue31313  han_meng_fei_sha 将一个应用apk放到手机的 /系统/应用  这个目录下, 就会是 系统应用.

  10. Java 操纵XML之修改XML文件

    Java 操纵XML之修改XML文件 一.JAVA DOM PARSER DOM interfaces The DOM defines several Java interfaces. Here ar ...