AVL树旋转

　　什么是AVL树？

　　AVL树是带有平衡条件的二叉查找树，一颗AVL树首先是二叉查收树（每个节点如果有左子树或右子树，那么左子树中数据小于该节点数据，右子树数据大于该节点数据），其次，AVL树必须满足平衡条件：每个节点的左子树和右子树的高度最多相差1（空树的高度定义为-1）。

　　

　　什么是旋转？AVL树为什么需要用到旋转？

　　由于AVL树本身的性质，当我们插入节点时，有可能会破坏AVL树的平衡性，使一棵树的左子树和右子树的高度相差大于1，此时就需要对树进行一些简单的修正来恢复其性质，这个修正的过程就叫做旋转。

　　我们来看一个简单的例子，比如这棵树，他在插入节点之后不满足AVL树的性质，这时我们可以使用一个旋转来使他成为一颗AVL树。

　　旋转前：　　　　　　　　　　　　　　　　　　　　3

　　　　　　　　　　　　　　　　　　　　　　　　　/

　　　　　　　　　　　　　　　　　　　　　　　　2

　　　　　　　　　　　　　　　　　　　　　　　/

　　　　　　　　　　　　　　　　　　　　　　1

　　这棵树根节点为3，插入2之后左右子树高度相差1，再插入1之后左右子树高度相差2（左子树高度为1，右子树高度为-1），此时这棵树不满足AVL树的条件，对这棵树进行旋转操作。

　　旋转后:　　　　　　　　　　　　　　　　　　　　2

　　　　　　　　　　　　　　　　　　　　　　　　/　　\

　　　　　　　　　　　　　　　　　　　　　　　1　　　　3

　　在经过一次旋转之后，这棵树的根节点为2，左右子树分别为1和3，满足AVL树的条件，插入完成。
　　

　　如何对结点进行旋转，使其满足AVL树的条件？

　　·单旋转：

　　当新插入的节点在二叉树的外侧（左子树的左侧或右子树的右侧），并且此时破坏了AVL树的平衡，我们使用一个单旋转来恢复AVL树的性质。

　　以左侧单旋转为例，比如刚才那个例子中，旋转前根节点为3，左子树高度为1，右子树高度为-1。此时我们先让左子树2的右子树（在这里为NULL）变为根节点的新左子树

　　　　　　　　　　　　　　　　　　　　　　　　　　　　 3

　　　　　　　　　　　　　　　　　　2　　　　　　　　　/　　\

　　　　　　　　　　　　　　　　/　　　　　　　　　NULL　　　　NULL

　　　　　　　　　　　　　　　1

　　再让原来的根节点3变为节点2的右子树

　　　　　　　　　　　　　　　　　　　　　　　　　　2

　　　　　　　　　　　　　　　　　　　　　　　　　/   \

　　　　　　　　　　　　　　　　　　　　　　　　1　　　　3

　　此时可以算是完成了一次单旋转，2变为新的根节点。这个旋转后的树满足AVL树的条件。

　　左侧单旋转代码：

　　

 typedef struct TreeNode
 {
     ElementType Element;
     struct TreeNode *Left;
     struct TreeNode *Right;
     int Height;
 }*AvlTree;
 int NodeHeight(AvlTree P)
 {
     if(P == NULL) return -;
     else return P->Height;
 }
 AvlTree SingleRotateWithLeft(AvlTree T)
 {
     /* T指向原来的根节点，T1指向旋转后的根节点 */
      AvlTree T1;
      T1 = T->Left;

     /* 根节点的左子树等于其原来左子树的右子树 */
     T->Left = T1->Right;

     /* 让原来的根节点成为新的根节点的右子树 */
     T1->Right = T;

     /* 重新设置节点高度 */
     T->Height = Max(NodeHeight(T->Left),NodeHeight(T->Right))+;
     T1->Height = Max(NodeHeight(T1->Left),T->Height)+;

     /* 将新的根节点返回 */
     return T1;
 }

　　右侧单旋转和左侧差不多：

　　　　　　　　　　1　　　　　　　　　　　　　　　　　　　　　　　　　　1

　　　　　　　　　　　\　　　　　　　　　　　　　　　　　　　　　　　　/　　　\

　　　　　　　　　　　　2　　　　　　　　　　　　　　　　　　　　　　2　　　　3

　　　　　　　　　　　　　\

　　　　　　　　　　　　　  3

 AvlTree SingleRotateWithRight(AvlTree T)
 {
     AvlTree T1;
     T1 = T->Right;
     T->Right = T1->Left;
     T1->Left = T;
     T->Height = Max(NodeHeight(T->left),NodeHeight(T->Right))+;
     T1->Height = Max(T->Height,NodeHeight(T1->Right))+;
     return T1;
 }

　　·双旋转

　　当新插入的节点在二叉树的内侧（左子树的右侧或右子树的左侧），并且此时破坏了AVL树的平衡，我们使用一个单旋转来恢复AVL树的性质。

　　这里还是先以左侧双旋转为例，我们来尝试建立一棵树并初始化，并设根节点为3

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　3

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　/　　\

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　NULL　　NULL

　　我们插入一个1，由于这个树应满足二叉查找树的条件，所以1应该插入根节点3的左侧

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　3

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　/　　\

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　1　　　　NULL

　　再插入一个2，由二叉查找树条件，2应该插在1的右侧

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　3

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　/　　\

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　1　　　　NULL

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　\

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　2

　　此时，由于根节点左子树和右子树高度相差大于一，所以此时不满足AVL树的条件，此时需要一个双旋转来使这棵树成为AVL树

　　首先，我们对根节点的左子树1进行右侧单旋转：

　　（根据单旋转的方法，令 1 的右子树等于原来右子树 2 的左子树 NULL ，再让 1 成为 2 的左子树，原来指向 1 的指针指向 2）

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　3

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　/　

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　2

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　/　

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　1　　　

　　然后，再对根节点3进行左侧单旋转：

　　（根据单旋转的方法，令 3 的左子树等于原来左子树 2 的右子树 NULL ，再让 3 成为 2 的右子树，2成为根节点）

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　2

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　/　　\

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 1　　　3

　　此时，完成了一个双旋转，这棵树满足AVL树的条件。

　　看代码：

 AvlTree DoubleRotateWithLeft(AvlTree T)
 {
     // 在根节点的左子树进行右侧单旋转
     T->Left = SingleRotateWithRight(T->Left);

     // 在根节点处进行左侧单旋转
     return SingleRotateWithLeft(T);
 }

　　在右侧进行双旋转和左侧类似：

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　1

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　\

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  3

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　/

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　2

　　对根节点的右子树进行左侧单旋转：

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　1

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　\

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　   2

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　\

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　3

　　对根节点进行右侧单旋转：

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　2

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　/　　 \

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　1　　　  3

　　

 AvlTree DoubleRotateWithRight(AvlTree T)
 {
     // 在T的右子树进行左侧单旋转
     T->Right = SingleRotateWithLeft(T->Right);

     // 在根节点T处进行右侧单旋转
     return SingleRotateWithRight(T);
 }

　　至此，我们已经看到了AVL树的四种旋转（左右单旋转，左右双旋转），有了这些旋转的方法，我们就可以在插入节点时进行判断，判断当前插入节点之后的树是否需要进行旋转，以及需要哪种旋转，进而实现任意在AVL树中插入节点。

　　具体的插入节点代码实现不在这里放出，可以参考《数据结构与算法分析-C语言描述版》（本文中的观点与代码大都来自此书，稍有改动，加入自己的理解）。

　　看一下代码实现后的运行结果：

　　

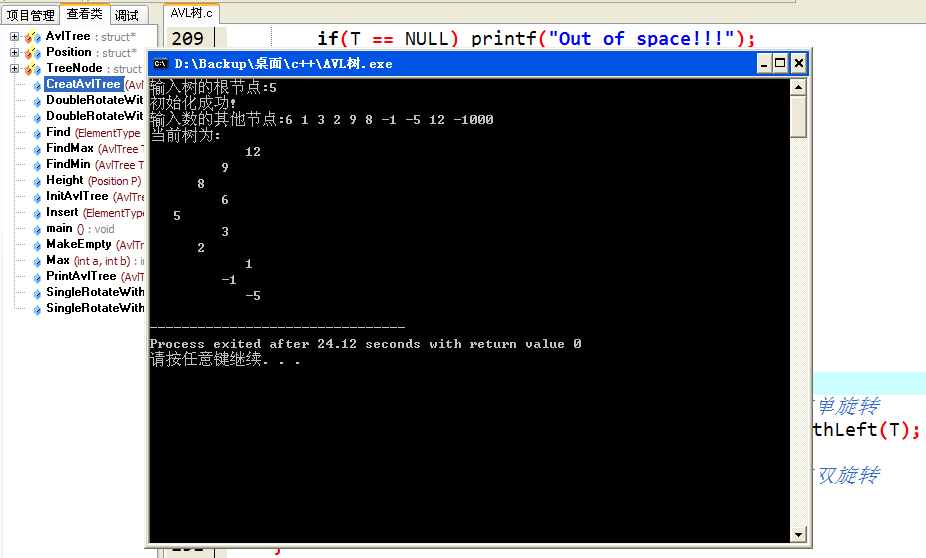
　　注： 这里输入的最后一个参数 -1000 是输入的结束条件，输出的树是逆时针旋转90°之后的树。