[MIT6.006] 9. Table Doubling, Karp-Rabin 双散列表， Karp-Rabin

在整理课程笔记前，先普及下课上没细讲的东西，就是下图，如果有个操作g(x)，它最糟糕的时间复杂度为Ο(c₂ * n)，它最好时间复杂度是Ω(c₁ * n)，那么θ则为Θ(n)。简单来说：如果O和Ω可以用同一个多项式表示，这里为c * n，那么这个多项式n就是我们所要求的渐进紧的界θ了：

上节课我们讲了下图的散列表：

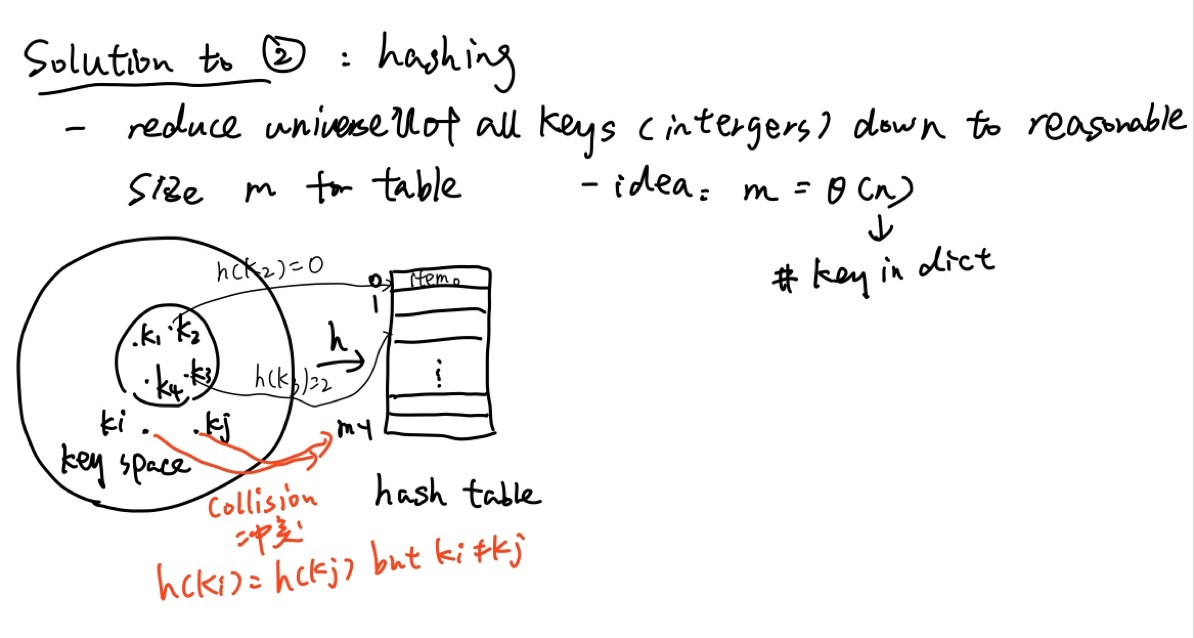
有个问题就是怎么去选择散列表的大小m？

有个方法就是先假设从一个小的m=8开始，然后按照需求进行增长/缩短。

这里举个例子：如果n > m (n为key space的大小，m为散列表大小)，那么应该增加散列表。方法有以下两种：

由上图可见双散列表更加节省时间。

关于双散列表的渐进紧界θ，如下图所示（这块其实我没怎么听太懂，但关于删除那块，按照第二种方式会更加节省时间）

现在开始本课重要内容：如何实现字符串的查找？如下图所示：假设一个待查询字符串s是‘6.006’，在文本库t中找到s。

最简单的一个办法就是，遍历移动进行查找，但这样的效率太慢了。如果想要更快的实现查找，先了解一个叫Rolling Hash的ADT（Abstract Data Type）：

简单来说，先提前定一个字符串r（其长度为待查字符串s），先往r里加入文本库t里前|s|个字符串，然后去哈希值，然后与s的哈希值对比，如果它们相等则标记当前r为匹配字段，如果它们不相同，r就追加后面的首元素，去掉r自己的首元素，相当于向右移动r的时候，保持r的长度不变，继续进行hash(r) 和 hash(s) 的比较。

但上面的方法有个问题，之前第8节课也提到，就是k₁≠k₂下，也可能会有冲突hash(k₁)=hash(k₂)出现，为了解决避免冲突，Karp-Rabin算法被提出来了：

具体的内容如上图，Karp-Rabin算法解决冲突的办法就是，当出现h(rs)=h(rt)相同时，再进一步对rs和rt对应位置上的字符串进行hash的对比，这样最后就能排除之前的冲突了。在该算法中采用了如下图的hash函数计算方式和append及skip的方式，它们的使用能更好的避免冲突：