CF1008D Pave the Parallelepiped

容斥原理

解法一：

其他容斥原理的题也可以用这种思想

---

先把$A$,$B$,$C$分解因数

一种很暴力的想法是，将这些因数分成若干个集合（画出韦恩图），然后对有序数组的三个数分别枚举其位于哪一个集合中

然后可以将这些因数划分成$7$个集合

$1$  $1$  $1$

$C$  $B$ $A$

此处为二进制下的数字

$001$:只为$A$的因数的集合

$010$:只为$B$的因数的集合

$100$:只为$C$的因数的集合

$011$:只为$A$,$B$的共同因数的集合

$101$:只为$A$,$C$的共同因数的集合

$110$:只为$B$,$C$的共同因数的集合

$111$:$A$,$B$,$C$的共同因数的集合

如图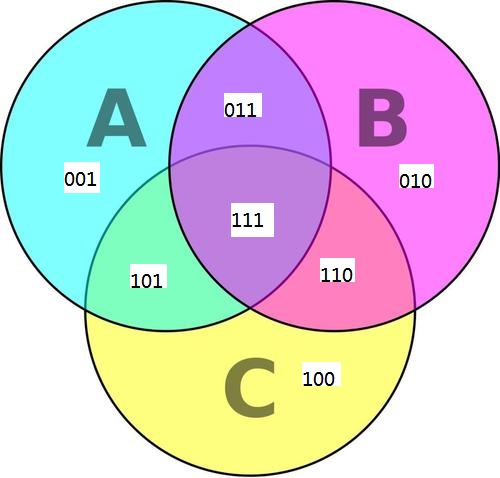

对于这几个集合所含数的个数可以在$O(\sqrt{x})$的时间内求出

还要注意因为题中长方体可以任意翻转，在枚举集合的时候要注意

枚举过$(i,j,k)$就不能再枚举$(i,k,j)$或$(j,k,i)$等其他情况

然后考虑如何统计

对于一个集合中有n个数来说，取出r可重复的元素的方案数为

$C_{n+r-1}^{r}$

此处同理

即可解决

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 const int N=1e5+100;
 4 int t,a,b,c,fac[8],ans,cnt[8];
 5 int ab,bc,ac,abc,sum[N];
 6 int cal(int x)
 7 {
 8     int cnt=0;
 9     for (int i=1;i*i<=x;i++)
10     {
11         if (x%i==0)
12         {
13             cnt++;
14             if (x/i!=i) cnt++;
15         }
16     }
17     return cnt;
18 }
19 int cal_fac(int x)
20 {
21     return sum[x];
22 }
23 int gcd(int a,int b)
24 {
25     if (b==0) return a;
26     return gcd(b,a%b);
27 }
28 bool check(int a,int b,int c)
29 {
30     //这个函数是判断a,b,c三个数任意排列是否分别为为A,B,C的因数
31     if ((a&1) && (b&2) && (c&4)) return true;
32     if ((a&1) && (c&2) && (b&4)) return true;
33     if ((b&1) && (a&2) && (c&4)) return true;
34     if ((b&1) && (c&2) && (a&4)) return true;
35     if ((c&1) && (b&2) && (a&4)) return true;
36     if ((c&1) && (a&2) && (b&4)) return true;
37     return false;
38 }
39 int C(int n,int m)
40 {
41     int cnt=1;
42     for (int i=n;i>n-m;i--)
43       cnt=cnt*i/(n-i+1);
44     return cnt;
45 }
46 int main()
47 {
48     for (int i=1;i<=1e5+10;i++)
49       sum[i]=cal(i);//要先预处理出范围内的因数个数
50     scanf("%d",&t);
51     while (t--)
52     {
53         scanf("%d%d%d",&a,&b,&c);;
54         memset(fac,0,sizeof(fac));
55         ans=0;
56         ab=gcd(a,b);ac=gcd(a,c);bc=gcd(b,c);
57         abc=gcd(a,gcd(b,c));
58         a=cal_fac(a);b=cal_fac(b);c=cal_fac(c);
59         ab=cal_fac(ab);ac=cal_fac(ac);bc=cal_fac(bc);
60         abc=cal_fac(abc);
61         fac[1]=a-ab-ac+abc;
62         fac[2]=b-ab-bc+abc;
63         fac[3]=ab-abc;
64         fac[4]=c-ac-bc+abc;
65         fac[5]=ac-abc;
66         fac[6]=bc-abc;
67         fac[7]=abc;//同上的定义
68         for (int i=1;i<=7;i++)
69         {
70             for (int j=i;j<=7;j++)
71             {
72                 for (int k=j;k<=7;k++)
73                 {
74                     if (check(i,j,k))
75                     {
76                         int sum=1;
77                         memset(cnt,0,sizeof(cnt));
78                         cnt[i]++;cnt[j]++;cnt[k]++;//统计每一个集合中要选取多少个数
79                         for (int p=1;p<=7;p++)
80                           sum=sum*C(fac[p]+cnt[p]-1,cnt[p]);//统计答案
81                         ans+=sum;
82                     }
83                 }
84             }
85         }
86         printf("%d\n",ans);
87     }
88 }

解法二：

直接容斥原理硬推公式，待填