数据结构之最小生成树Prim算法
普里姆算法介绍
普里姆(Prim)算法,是用来求加权连通图的最小生成树算法
基本思想:对于图G而言,V是所有顶点的集合;现在,设置两个新的集合U和T,其中U用于存放G的最小生成树中的顶点,T存放G的最小生成树中的边。 从所有uЄU,vЄ(V-U) (V-U表示出去U的所有顶点)的边中选取权值最小的边(u, v),将顶点v加入集合U中,将边(u, v)加入集合T中,如此不断重复,直到U=V为止,最小生成树构造完毕,这时集合T中包含了最小生成树中的所有边。
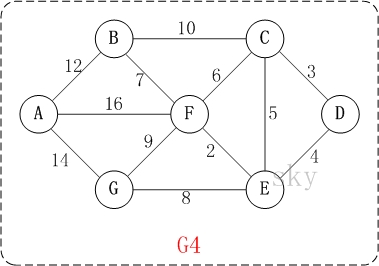
代码实现
1. 思想逻辑
(1)以无向图的某个顶点(A)出发,计算所有点到该点的权重值,若无连接取最大权重值#define INF (~(0x1<<31))
(2)找到与该顶点最小权重值的顶点(B),再以B为顶点计算所有点到改点的权重值,依次更新之前的权重值,注意权重值为0或小于当前权重值的不更新,因为1是一当找到最小权重值的顶点时,将权重值设为了0,2是会出现无连接的情况。
(3)将上述过程一次循环,并得到最小生成树。
2. Prim算法
// Prim最小生成树
void Prim(int nStart)
{
int i = ;
int nIndex=; // prim最小树的索引,即prims数组的索引
char cPrims[MAX]; // prim最小树的结果数组
int weights[MAX]; // 顶点间边的权值 cPrims[nIndex++] = m_mVexs[nStart].data; // 初始化"顶点的权值数组",
// 将每个顶点的权值初始化为"第start个顶点"到"该顶点"的权值。
for (i = ; i < m_nVexNum; i++)
{
weights[i] = GetWeight(nStart, i);
} for (i = ; i < m_nVexNum; i ++)
{
if (nStart == i)
{
continue;
} int min = INF;
int nMinWeightIndex = ;
for (int k = ; k < m_nVexNum; k ++)
{
if (weights[k]!= && weights[k] < min)
{
min = weights[k];
nMinWeightIndex = k;
}
} // 找到下一个最小权重值索引
cPrims[nIndex++] = m_mVexs[nMinWeightIndex].data;
// 以找到的顶点更新其他点到该点的权重值
weights[nMinWeightIndex]=;
int nNewWeight = ;
for (int ii = ; ii < m_nVexNum; ii++)
{
nNewWeight = GetWeight(nMinWeightIndex, ii);
// 该位置需要特别注意
if ( != weights[ii] && weights[ii] > nNewWeight)
{
weights[ii] = nNewWeight;
}
}
}
// 计算最小生成树的权重值
int nSum = ;
for (i = ; i < nIndex; i ++)
{
int min = INF;
int nVexsIndex = GetVIndex(cPrims[i]);
for (int kk = ; kk < i; kk ++)
{
int nNextVexsIndex = GetVIndex(cPrims[kk]);
int nWeight = GetWeight(nVexsIndex, nNextVexsIndex);
if (nWeight < min)
{
min = nWeight;
}
}
nSum += min;
} // 打印最小生成树
cout << "PRIM(" << m_mVexs[nStart].data <<")=" << nSum << ": ";
for (i = ; i < nIndex; i++)
cout << cPrims[i] << " ";
cout << endl; }
3. 全部实现
#include "stdio.h"
#include <iostream>
using namespace std; #define MAX 100
#define INF (~(0x1<<31)) // 最大值(即0X7FFFFFFF) class EData
{
public:
EData(char start, char end, int weight) : nStart(start), nEnd(end), nWeight(weight){} char nStart;
char nEnd;
int nWeight;
};
// 边
struct ENode
{
int nVindex; // 该边所指的顶点的位置
int nWeight; // 边的权重
ENode *pNext; // 指向下一个边的指针
}; struct VNode
{
char data; // 顶点信息
ENode *pFirstEdge; // 指向第一条依附该顶点的边
}; // 无向邻接表
class listUDG
{
public:
listUDG(){};
listUDG(char *vexs, int vlen, EData **pEData, int elen)
{
m_nVexNum = vlen;
m_nEdgNum = elen; // 初始化"邻接表"的顶点
for (int i = ; i < vlen; i ++)
{
m_mVexs[i].data = vexs[i];
m_mVexs[i].pFirstEdge = NULL;
} char c1,c2;
int p1,p2;
ENode *node1, *node2;
// 初始化"邻接表"的边
for (int j = ; j < elen; j ++)
{
// 读取边的起始顶点和结束顶点
c1 = pEData[j]->nStart;
c2 = pEData[j]->nEnd;
p1 = GetVIndex(c1);
p2 = GetVIndex(c2); node1 = new ENode();
node1->nVindex = p2;
node1->nWeight = pEData[j]->nWeight;
if (m_mVexs[p1].pFirstEdge == NULL)
{
m_mVexs[p1].pFirstEdge = node1;
}
else
{
LinkLast(m_mVexs[p1].pFirstEdge, node1);
} node2 = new ENode();
node2->nVindex = p1;
node2->nWeight = pEData[j]->nWeight;
if (m_mVexs[p2].pFirstEdge == NULL)
{
m_mVexs[p2].pFirstEdge = node2;
}
else
{
LinkLast(m_mVexs[p2].pFirstEdge, node2);
}
} }
~listUDG()
{
ENode *pENode = NULL;
ENode *pTemp = NULL;
for (int i = ; i < m_nVexNum; i ++)
{
pENode = m_mVexs[i].pFirstEdge;
if (pENode != NULL)
{
pTemp = pENode;
pENode = pENode->pNext; delete pTemp;
}
delete pENode;
}
} void PrintUDG()
{
ENode *pTempNode = NULL;
cout << "邻接无向表:" << endl;
for (int i = ; i < m_nVexNum; i ++)
{
cout << "顶点:" << GetVIndex(m_mVexs[i].data)<< "-" << m_mVexs[i].data<< "->";
pTempNode = m_mVexs[i].pFirstEdge;
while (pTempNode)
{
cout <<pTempNode->nVindex << "->";
pTempNode = pTempNode->pNext;
}
cout << endl;
}
} // Prim最小生成树
void Prim(int nStart)
{
int i = ;
int nIndex=; // prim最小树的索引,即prims数组的索引
char cPrims[MAX]; // prim最小树的结果数组
int weights[MAX]; // 顶点间边的权值 cPrims[nIndex++] = m_mVexs[nStart].data; // 初始化"顶点的权值数组",
// 将每个顶点的权值初始化为"第start个顶点"到"该顶点"的权值。
for (i = ; i < m_nVexNum; i++)
{
weights[i] = GetWeight(nStart, i);
} for (i = ; i < m_nVexNum; i ++)
{
if (nStart == i)
{
continue;
} int min = INF;
int nMinWeightIndex = ;
for (int k = ; k < m_nVexNum; k ++)
{
if (weights[k]!= && weights[k] < min)
{
min = weights[k];
nMinWeightIndex = k;
}
} // 找到下一个最小权重值索引
cPrims[nIndex++] = m_mVexs[nMinWeightIndex].data;
// 以找到的顶点更新其他点到该点的权重值
weights[nMinWeightIndex]=;
int nNewWeight = ;
for (int ii = ; ii < m_nVexNum; ii++)
{
nNewWeight = GetWeight(nMinWeightIndex, ii);
// 该位置需要特别注意
if ( != weights[ii] && weights[ii] > nNewWeight)
{
weights[ii] = nNewWeight;
}
}
}
// 计算最小生成树的权重值
int nSum = ;
for (i = ; i < nIndex; i ++)
{
int min = INF;
int nVexsIndex = GetVIndex(cPrims[i]);
for (int kk = ; kk < i; kk ++)
{
int nNextVexsIndex = GetVIndex(cPrims[kk]);
int nWeight = GetWeight(nVexsIndex, nNextVexsIndex);
if (nWeight < min)
{
min = nWeight;
}
}
nSum += min;
} // 打印最小生成树
cout << "PRIM(" << m_mVexs[nStart].data <<")=" << nSum << ": ";
for (i = ; i < nIndex; i++)
cout << cPrims[i] << " ";
cout << endl;
}
private:
// 获取<start, end>的权值,若start和end不是连接的,则返回无穷大
int GetWeight(int start, int end)
{
if (start == end)
{
return ;
}
ENode *pTempNode = m_mVexs[start].pFirstEdge;
while (pTempNode)
{
if (end == pTempNode->nVindex)
{
return pTempNode->nWeight;
}
pTempNode = pTempNode->pNext;
} return INF;
} // 返回顶点的索引
int GetVIndex(char ch)
{
int i = ;
for (; i < m_nVexNum; i ++)
{
if (m_mVexs[i].data == ch)
{
return i;
}
}
return -;
} void LinkLast(ENode *pFirstNode, ENode *pNode)
{
if (pFirstNode == NULL || pNode == NULL)
{
return;
}
ENode *pTempNode = pFirstNode;
while (pTempNode->pNext != NULL)
{
pTempNode = pTempNode->pNext;
} pTempNode->pNext = pNode;
} private:
int m_nVexNum; // 顶点数目
int m_nEdgNum; // 边数目
VNode m_mVexs[MAX];
VNode m_PrimVexs[MAX];
}; void main()
{
char vexs[] = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
// 边
EData *edges[] = {
// 起点 终点 权
new EData('A', 'B', ),
new EData('A', 'F', ),
new EData('A', 'G', ),
new EData('B', 'C', ),
new EData('B', 'F', ),
new EData('C', 'D', ),
new EData('C', 'E', ),
new EData('C', 'F', ),
new EData('D', 'E', ),
new EData('E', 'F', ),
new EData('E', 'G', ),
new EData('F', 'G', )
};
int vlen = sizeof(vexs)/sizeof(vexs[]);
int elen = sizeof(edges)/sizeof(edges[]);
listUDG* pG = new listUDG(vexs, vlen, edges, elen); pG->PrintUDG(); // 打印图
pG->Prim(); for (int i = ; i < elen; i ++)
{
delete edges[i];
}
return;
}
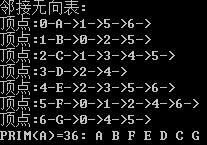
数据结构之最小生成树Prim算法的更多相关文章
- 数据结构:最小生成树--Prim算法
最小生成树:Prim算法 最小生成树 给定一无向带权图.顶点数是n,要使图连通仅仅需n-1条边.若这n-1条边的权值和最小,则称有这n个顶点和n-1条边构成了图的最小生成树(minimum-cost ...
- 数据结构代码整理(线性表,栈,队列,串,二叉树,图的建立和遍历stl,最小生成树prim算法)。。持续更新中。。。
//归并排序递归方法实现 #include <iostream> #include <cstdio> using namespace std; #define maxn 100 ...
- 最小生成树Prim算法(邻接矩阵和邻接表)
最小生成树,普利姆算法. 简述算法: 先初始化一棵只有一个顶点的树,以这一顶点开始,找到它的最小权值,将这条边上的令一个顶点添加到树中 再从这棵树中的所有顶点中找到一个最小权值(而且权值的另一顶点不属 ...
- 最小生成树—prim算法
最小生成树prim算法实现 所谓生成树,就是n个点之间连成n-1条边的图形.而最小生成树,就是权值(两点间直线的值)之和的最小值. 首先,要用二维数组记录点和权值.如上图所示无向图: int map[ ...
- Highways POJ-1751 最小生成树 Prim算法
Highways POJ-1751 最小生成树 Prim算法 题意 有一个N个城市M条路的无向图,给你N个城市的坐标,然后现在该无向图已经有M条边了,问你还需要添加总长为多少的边能使得该无向图连通.输 ...
- SWUST OJ 1075 求最小生成树(Prim算法)
求最小生成树(Prim算法) 我对提示代码做了简要分析,提示代码大致写了以下几个内容 给了几个基础的工具,邻接表记录图的一个的结构体,记录Prim算法中最近的边的结构体,记录目标边的结构体(始末点,值 ...
- 图论算法(五)最小生成树Prim算法
最小生成树\(Prim\)算法 我们通常求最小生成树有两种常见的算法--\(Prim\)和\(Kruskal\)算法,今天先总结最小生成树概念和比较简单的\(Prim\)算法 Part 1:最小生成树 ...
- 最小生成树,Prim算法与Kruskal算法,408方向,思路与实现分析
最小生成树,Prim算法与Kruskal算法,408方向,思路与实现分析 最小生成树,老生常谈了,生活中也总会有各种各样的问题,在这里,我来带你一起分析一下这个算法的思路与实现的方式吧~~ 在考研中呢 ...
- 最小生成树--Prim算法,基于优先队列的Prim算法,Kruskal算法,Boruvka算法,“等价类”UnionFind
最小支撑树树--Prim算法,基于优先队列的Prim算法,Kruskal算法,Boruvka算法,“等价类”UnionFind 最小支撑树树 前几节中介绍的算法都是针对无权图的,本节将介绍带权图的最小 ...
随机推荐
- alias指令别名和 sshpass命令简化ssh登陆
在之前的一篇博文中 ubuntu下关于profile和bashrc中环境变量的理解 提到过可以编辑bashrc文件,vim ~/.bashrc,来编写自己的小指令,就是给长指令取个简单的别名.比如b ...
- docker 中安装PHP扩展
可以通过两种方式实现 1.pecl pdo_msql 方式二: docker-php-ext-install pdo pdo_mysql 如果报 /usr/local/bin/docker-php-e ...
- 深入解析Koa之核心原理
这篇文章主要介绍了玩转Koa之核心原理分析,本文从封装创建应用程序函数.扩展res和req.中间件实现原理.异常处理的等这几个方面来介绍,写的十分的全面细致,具有一定的参考价值,对此有需要的朋友可以参 ...
- 20145109《Java程序设计》第一周学习总结
20145109 <Java程序设计>第一周学习总结 教材学习内容总结 About JVM, JRE, JDK JVM包含于JRE中,用于运行Java程序.JDK用于开发Java程序,包含 ...
- C++中int转为char 以及int 转为string和string 转int和字符串的split
1.对于int 转为char 直接上代码: 正确做法: void toChar(int b) { char u; ]; _itoa( b, buffer, ); //正确解法一 u = buffer[ ...
- sql 加密解密函数
if object_ID ( 'fn_ACITEncryption' ) is not null drop function fn_ACITEncryption go create ...
- 安装 SPRING TOOL SUITE
- Java编程时部分快捷键
alt + / 内容助理 配置:Window->properties->keys->查看alt + /的配置,然后解除当前的配置->搜索content assist->解 ...
- Pandas选项和自定义
Pandas提供API来自定义其行为的某些方面,大多使用来显示. API由五个相关函数组成.它们分别是 - get_option() set_option() reset_option() descr ...
- JNI_Z_07_方法的操作(没有String类型的参数)_参数的传递方式
1. 2.VC6(CPP)的DLL代码: #include<stdio.h> #include "jniZ_TjniMethod02.h" JNIEXPORT void ...
